
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
At a certain store for a certain month, in a chart given below, the pr
[#permalink]
 30 Sep 2021, 05:32
30 Sep 2021, 05:32
Expert Reply
3
Bookmarks
Question Stats:
 50% (02:10) correct
50% (02:10) correct
 50% (01:53) wrong
50% (01:53) wrong  based on 10 sessions
based on 10 sessions
Hide Show timer Statistics
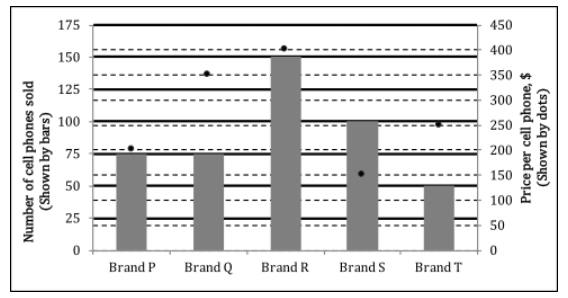
At a certain store for a certain month, in a chart given below, the price per cell phone (in dollars) is shown by dots (read from right hand side vertical axis) and the number of cell phones sold (read from left hand side vertical axis).
GRE What is the median price of the cell phones sold by the store in that month.jpg [ 70.29 KiB | Viewed 5087 times ]
What is the median price of the cell phones sold by the store in that month
Source: manhattanreview
Attachment:
GRE What is the median price of the cell phones sold by the store in that month.jpg [ 70.29 KiB | Viewed 5087 times ]
What is the median price of the cell phones sold by the store in that month
Show: :: OA
300
Source: manhattanreview
Re: At a certain store for a certain month, in a chart given below, the pr
[#permalink]
 30 Sep 2021, 09:04
30 Sep 2021, 09:04
1
The question is about the median price, so writing as a table with price ascending
Brand Quantity Price
S 100 $150
P 75 $200
T 50 $250
Q 75 $300
R 150 $400
Total number of phones sold is 450 so the median price is average of 225th and 226th phone and in this case it's Brand T and Q, ($250 + $ 350)/2 = $300
Brand Quantity Price
S 100 $150
P 75 $200
T 50 $250
Q 75 $300
R 150 $400
Total number of phones sold is 450 so the median price is average of 225th and 226th phone and in this case it's Brand T and Q, ($250 + $ 350)/2 = $300
At a certain store for a certain month, in a chart given below, the pr
[#permalink]
 30 Sep 2021, 10:08
30 Sep 2021, 10:08
1
Could someone please tell me why is arranging the 5 prices alone in ascending order of price ( S P T Q R) and seeing the middle value (T) to be the median wrong. and in which case ( how would the question be worded) would this be the required method of solving.







