AkkuJi
Here is my explanation

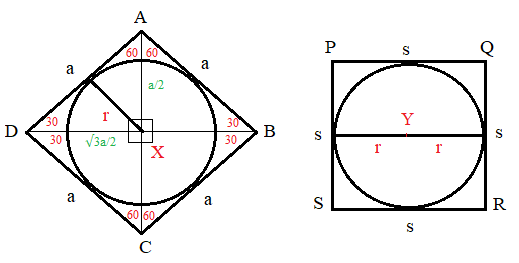
Let the square sheet PQRS have all sides as $s$
Area of circle Y with radius $r$ insribed in it would be $\frac{πs^2}{4}$

Remember - Equilateral parallelogram is a Rhombus

Let the rhombus sheet ABCD have all sides as $a$
(Refer to the figure below)

In △AXD;
∠DAX = 60°
∠ADX = 30°
∠AXD = 90° (since, diagonals of a rhombus are perpendicular)

Using the 30°-60°-90° property;
AX (opposite to 30°) = $\frac{a}{2}$
DX (opposite to 60°) = $\frac{\sqrt{3}a}{2}$

In order to find the radius of circle X inscribed in rhombus ABCD, we can equate the area in △AXD
i.e. $\frac{1}{2}(\frac{a}{2})(\frac{\sqrt{3}a}{2}) = \frac{1}{2}(a)(r)$
$\frac{\sqrt{3}a^2}{4} = ar$
$r = \frac{\sqrt{3}a}{4}$

We have been given - the areas of the two circles will be equal
So, $π(\frac{\sqrt{3}a}{4})^2 = \frac{πs^2}{4}$
$\frac{3a^2}{16} = \frac{s^2}{4}$
$\frac{3a^2}{4} = s^2$
$s = \frac{\sqrt{3}a}{2}$


Now, Area of rhombus ABCD = $\frac{1}{2}$x diagonal AC x diagonal BD = $\frac{1}{2}(a)(\sqrt{3}a) = \frac{\sqrt{3}a^2}{2}$, and
Area of square PQRS = $s^2 = (\frac{\sqrt{3}a}{2})^2 = \frac{3a^2}{4}$

Required ratio = $(\frac{\sqrt{3}}{2})(\frac{4}{3}) = \frac{2}{\sqrt{3}}$

Thanks for the explanation KarunMendiratta

Hello from the GRE Prep Club BumpBot!

Thanks to another GRE Prep Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).

Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.