Explanation



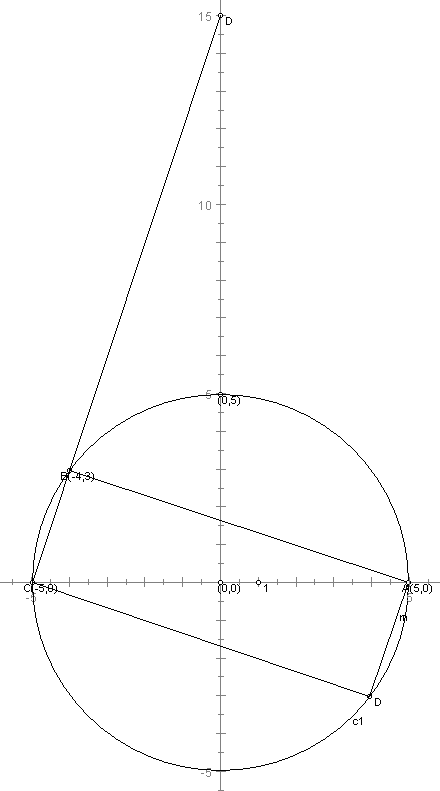
Let's see what has been provided in the question.

Circle's equation: $x^2+y^2=5^2$
Circle has a radius of 5 and is centered at (0,0)

AC is the diagonal of the rectangle and lies on x-axis; means AC=10

B lies in 2nd quadrant and D lies in 4th quadrant. See the image.

BC lies on line "y=3x+15". B and C are two vertices of the rectangle. We can find B and C if we find the solutions for x and y for both line and circle. Line y=3x+15 must intersect the circle on two points giving us the vertices B and C. These two points can be found by solving the simultaneous equations for the circle and the line.

Line: $y=3x+15$ ------ 1
Circle: $y^2+x^2=25$ ------ 2

Substituting 1 in 2:
$(3x+15)^2+x^2=25$
$9x^2+225+90x+x^2=25$
$10x^2+200+90x=0$
$x^2+9x+20=0$
$x^2+9x+20=0$
$(x+5)(x+4)=0$
x=-5 and x=-4

if x=-5; y= 3x+15 = 3*(-5)+15=0
if x=-4; y= 3x+15 = 3*(-4)+15=3

We found the vertices B and C now; B(-4,3) and C(-5,0)

Length of BC;
Distance between two points $(x_1,y_1) and (x_2,y_2)$ is found using following formula:
$BC = sqrt{(y_2-y_1)^2+(x_2-x_1)^2}$

Distance between B(-4,3) and C(-5,0)
$BC = sqrt{(0-3)^2+(-5-(-4))^2} = sqrt{9+1} = sqrt{10}$

We now know $BC=sqrt{10} & AC=10$

We can find AB; $\triangle{ABC}$ is a right angled triangle with hypotenuse as AC. We can use Pythagoras theorem to find AB

$(AC)^2=(AB)^2+(BC)^2$
$10^2=(AB)^2+(\sqrt{10})^2$
$100=(AB)^2+10$
$(AB)^2=100-10=90$
$AB=\sqrt{90}$

Area of the rectangle ABCD
$BC*AB = \sqrt{10}*\sqrt{90} = \sqrt{900} = 30$

Ans: "B"