
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
A surveyor is looking at two buildings from a distance, both of which
[#permalink]
 11 Aug 2022, 10:38
11 Aug 2022, 10:38
Expert Reply
Question Stats:
 100% (02:23) correct
100% (02:23) correct
 0% (00:00) wrong
0% (00:00) wrong  based on 6 sessions
based on 6 sessions
Hide Show timer Statistics
Very Hard
A surveyor is looking at two buildings from a distance, both of which stand perpendicular to the ground. He sets two telescopes up at 45° angles to the tops of both buildings, and both telescopes an elevation of 100 feet above sea level. The surveyor knows that the bases of both buildings are 100 feet above sea level and that the top of building A is 1,100 feet above sea level. The telescope pointing at building A is 250 feet away from the base of the building. The telescope pointing at building B is 300 feet away from the base of that building.
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
A surveyor is looking at two buildings from a distance, both of which stand perpendicular to the ground. He sets two telescopes up at 45° angles to the tops of both buildings, and both telescopes an elevation of 100 feet above sea level. The surveyor knows that the bases of both buildings are 100 feet above sea level and that the top of building A is 1,100 feet above sea level. The telescope pointing at building A is 250 feet away from the base of the building. The telescope pointing at building B is 300 feet away from the base of that building.
Quantity A |
Quantity B |
the height of building A |
The height of building B |
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Part of the project: GRE Quantitative Comparison GEOMETRY+Tricky Questions - Special Summer Edition (2022)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
GRE Math Essentials (2022)
GRE Geometry Formulas
GRE - Math Book
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
GRE Math Essentials (2022)
GRE Geometry Formulas
GRE - Math Book
A surveyor is looking at two buildings from a distance, both of which
[#permalink]
 21 Aug 2022, 01:34
21 Aug 2022, 01:34
Expert Reply
OE
Quote:
The problem states that both buildings are built at the same
elevation and are perpendicular to the ground, and that both
telescopes are level with the bases of the buildings and pointed
at angles of 45° to the tops of the buildings. This means that
similar 45/45/90 right triangles are created because the third
angle in each triangle can only be 45°. A ratio can be set up to
determine the height of building B based on the height of
building A and the distance from the bases of the buildings to
their respective telescopes. Note that the telescopes are 100 ft
above sea level and subtract that amount from the height of the
top of building A to get its actual height. Let b represent the
height of building B in feet:
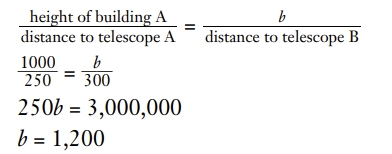
screenshot.805.jpg [ 32.52 KiB | Viewed 1485 times ]
The height of building B is 1,200 feet. This is more than the
height of building A (1,000) so the answer is b.
Note: It is not necessary to solve for b because it is evident that
b > 1,000 from looking at the proportion.
elevation and are perpendicular to the ground, and that both
telescopes are level with the bases of the buildings and pointed
at angles of 45° to the tops of the buildings. This means that
similar 45/45/90 right triangles are created because the third
angle in each triangle can only be 45°. A ratio can be set up to
determine the height of building B based on the height of
building A and the distance from the bases of the buildings to
their respective telescopes. Note that the telescopes are 100 ft
above sea level and subtract that amount from the height of the
top of building A to get its actual height. Let b represent the
height of building B in feet:
Attachment:
screenshot.805.jpg [ 32.52 KiB | Viewed 1485 times ]
The height of building B is 1,200 feet. This is more than the
height of building A (1,000) so the answer is b.
Note: It is not necessary to solve for b because it is evident that
b > 1,000 from looking at the proportion.
A surveyor is looking at two buildings from a distance, both of which
[#permalink]
 21 Aug 2022, 01:34
21 Aug 2022, 01:34
Expert Reply




