
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Question 18: In the figure above, A and b are the centers of
[#permalink]
 19 May 2016, 16:21
19 May 2016, 16:21
3
Bookmarks
Question Stats:
 45% (02:12) correct
45% (02:12) correct
 54% (03:58) wrong
54% (03:58) wrong  based on 11 sessions
based on 11 sessions
Hide Show timer Statistics
Attachment:
GRe gemotery circle.jpg [ 33.33 KiB | Viewed 2834 times ]
In the figure above, A and B are the centers of the two circles. If each circle has radius X, what is the area of the shaded region?
A. \(\frac{(2\pi - \sqrt{3}) x^2}{6}\)
B. \(\frac{(4\pi - 3 \sqrt{3}) x^2}{12}\)
C. \(\frac{(4\pi - 3 \sqrt{3}) x^2}{6}\)
D. \(\frac{(4\pi - \sqrt{3}) x^2}{6}\)
E. \(\frac{(6\pi - 1) x^2}{6}\)
Re: Question 18: In the figure above, A and b are the centers of
[#permalink]
 23 May 2016, 14:51
23 May 2016, 14:51
2
1
Expert Reply
Solution
Here we have two circles with centers A and B they intersect on points say X and Y. Now to find the area of the shaded region.
Let us connect the points X, A, B to form a triangle and Y, A, B to form another triangle. Since the radius of circle A and B are same. We can say that XAB is an equilateral triangle. With XA=AB= XB= radius of circle. Similarly YAB is also a triangle.
So now we can clearly see that the area of the two triangles = \(2*\sqrt{3}*\frac{x^2}{4}\). ........(i)
Now the segment, i.e. the area between the triangle and a circle.
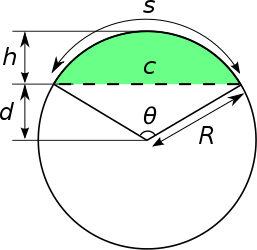
Area of segment = \(\frac{x^2}{2}(\frac{pi*theta}{180}- sin(theta))\).
Where theta is the central angle.
Or in our case angle XAB = 60 degrees= theta.
Putting theta = 60 we have
Area of segment= \(\frac{pi*x^2}{6} - \sqrt{3}\frac{x^2}{2}\).
Now we have 4 such segments. Now adding this to (i) and simplifying we get
Area of the shaded region as = \(\frac{4*pi}{6}*x^2 - 3*\sqrt{3}\frac{1}{2}*x^2\)
Here we have two circles with centers A and B they intersect on points say X and Y. Now to find the area of the shaded region.
Let us connect the points X, A, B to form a triangle and Y, A, B to form another triangle. Since the radius of circle A and B are same. We can say that XAB is an equilateral triangle. With XA=AB= XB= radius of circle. Similarly YAB is also a triangle.
So now we can clearly see that the area of the two triangles = \(2*\sqrt{3}*\frac{x^2}{4}\). ........(i)
Now the segment, i.e. the area between the triangle and a circle.

Area of segment = \(\frac{x^2}{2}(\frac{pi*theta}{180}- sin(theta))\).
Where theta is the central angle.
Or in our case angle XAB = 60 degrees= theta.
Putting theta = 60 we have
Area of segment= \(\frac{pi*x^2}{6} - \sqrt{3}\frac{x^2}{2}\).
Now we have 4 such segments. Now adding this to (i) and simplifying we get
Area of the shaded region as = \(\frac{4*pi}{6}*x^2 - 3*\sqrt{3}\frac{1}{2}*x^2\)
Re: Question 18: In the figure above, A and b are the centers of
[#permalink]
 23 May 2016, 20:24
23 May 2016, 20:24
2
Let us assume other two points of intersection of both circles are C and D. The distance between A and B is x. The line CD intersects AB at mid point and let us assume the point of intersection is E.
Now triangle AEC is 30, 60, 90 triangle. (sides x, x/2 and x*Square root of 3/2). Hence the arc CADB makes 120 degrees, so the area of arc CADB is 120/360*pi*x^2 = pi*x^2 / 3
Area of the triangle CAD is 1/2 * x * x*(Square root 3)/2.
The answer is two times (pi*x^2 / 3 - 1/2 * x * x*(Square root 3)/2). = (4 pi - 3*(Square root 3))*x^2/6. Hence C.
Now triangle AEC is 30, 60, 90 triangle. (sides x, x/2 and x*Square root of 3/2). Hence the arc CADB makes 120 degrees, so the area of arc CADB is 120/360*pi*x^2 = pi*x^2 / 3
Area of the triangle CAD is 1/2 * x * x*(Square root 3)/2.
The answer is two times (pi*x^2 / 3 - 1/2 * x * x*(Square root 3)/2). = (4 pi - 3*(Square root 3))*x^2/6. Hence C.







