GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Segment AC is the diameter of circle O with the length 10, and AB =
[#permalink]
18 Feb 2022, 08:00
18 Feb 2022, 08:00
1
Expert Reply
00:00
Question Stats:
75% (02:52) correct
25% (01:57) wrong based on 8 sessions
Hide Show timer Statistics
Segment AC is the diameter of circle O with the length 10, and AB = 5. Segment BD is the altitude drawn from B to AC. What is the length of BD?
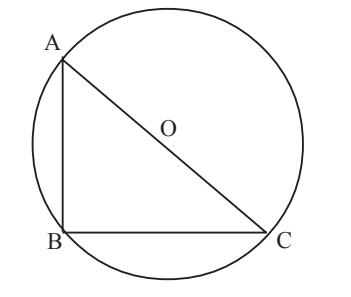
GRE Circle and triangle.jpg [ 20.94 KiB | Viewed 1422 times ]
(A) 5
(B) 5√3/2
(C) 2√10
(D) 3√5
(E) 3√10
Attachment:
GRE Circle and triangle.jpg [ 20.94 KiB | Viewed 1422 times ]
(A) 5
(B) 5√3/2
(C) 2√10
(D) 3√5
(E) 3√10
Retired Moderator
Joined: 16 Apr 2020
Status:Founder & Quant Trainer
Affiliations: Prepster Education
Posts: 1546
Given Kudos: 172
Location: India
WE:Education (Education)
Re: Segment AC is the diameter of circle O with the length 10, and AB =
[#permalink]
24 Feb 2022, 01:30
24 Feb 2022, 01:30
1
Carcass wrote:
Segment AC is the diameter of circle O with the length 10, and AB = 5. Segment BD is the altitude drawn from B to AC. What is the length of BD?
(A) 5
(B) 5√3/2
(C) 2√10
(D) 3√5
(E) 3√10
Attachment:
The attachment GRE Circle and triangle.jpg is no longer available
(A) 5
(B) 5√3/2
(C) 2√10
(D) 3√5
(E) 3√10
Attachment:
GRE Circle and triangle.jpg [ 16.33 KiB | Viewed 1236 times ]
Applying Pythagoras Theorem in \(ΔABC\);
\(AC^2 = AB^2 + BC^2\)
\(10^2 = 5^2 + BC^2\)
\(100 - 25 = BC^2\)
\(BC = \sqrt{75} = 5\sqrt{3}\)
Now, Area of \(ΔABC\) = \(\frac{1}{2}(AB)(BC)\) = \(\frac{1}{2}(AC)(BD)\)
\((AB)(BC) = (AC)(BO)\)
\((5)(5\sqrt{3}) = (10)(BD)\)
\(BD = \frac{5\sqrt{3}}{2}\)
Hence, option B
gmatclubot
Re: Segment AC is the diameter of circle O with the length 10, and AB = [#permalink]
24 Feb 2022, 01:30
Moderators:
