
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
The outer figure above is a rectangle with four rounded corn
[#permalink]
 22 Jul 2020, 10:39
22 Jul 2020, 10:39
Expert Reply
Question Stats:
 67% (01:12) correct
67% (01:12) correct
 32% (01:37) wrong
32% (01:37) wrong  based on 64 sessions
based on 64 sessions
Hide Show timer Statistics
Attachment:
GRE rectangle with a circle.jpg [ 22.66 KiB | Viewed 2967 times ]
The outer figure above is a rectangle with four rounded corners of radius equal to 2. The inner figure is a circle.
Quantity A |
Quantity B |
The shaded area |
30 |
A)The quantity in Column A is greater.
B)The quantity in Column B is greater.
C)The two quantities are equal.
D)The relationship cannot be determined from the information given.
The outer figure above is a rectangle with four rounded corn
[#permalink]
 17 Dec 2022, 12:29
17 Dec 2022, 12:29
1
Seeing this problem on first glance, my intuition told me that the answer was D. However, on the GRE it is best not to blindly trust our intuition; we should test our assumptions.
If figure was rectangle, then the area would be: 6 x 10 = 60. However, as the edges are rounded we must subtract them from the total:

rounded edges.png [ 60.71 KiB | Viewed 1857 times ]
So the rectangular figure has an approximate area of 60 - (16 - 4 pi ) = 56.566.
From here, we must subtract the area of the circle contained in the figure in order to determine the area of the shaded portion of the figure. As the figure is not drawn to scale, this will be a range of values.
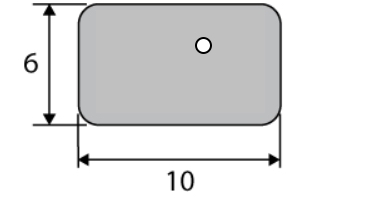
GRE rectangle with a circle-1.jpg [ 11.74 KiB | Viewed 1907 times ]
As the radius of the circle is not specified, it could theoretically be an infinitesimally small. Take for example a circle with a radius of 0.01. The area of the circle would be: (0.01)^2 pi = 0.0003. Even this value subtracted from the area of the rectangular figure would be negligible. Thus, we can say that the Area Max = 56.566
To find the minimum area of the shaded portion of the figure, we set the area of the inner circle to it's maximum value:
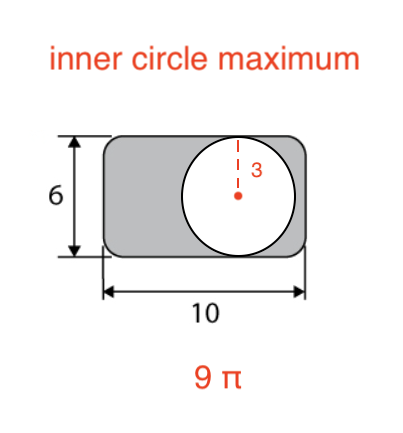
Inner circle max.png [ 29.77 KiB | Viewed 1882 times ]
Subtracting this value from the area of the rectangular figure we can find the minimum area:
56.566 - 3 pi = 28.292 ----> Area min = 28.292
28.292 < QA < 56.566
QB = 30
As QB falls within QA's range, we can confirm that Answer Choice D is correct.
If figure was rectangle, then the area would be: 6 x 10 = 60. However, as the edges are rounded we must subtract them from the total:
Attachment:
rounded edges.png [ 60.71 KiB | Viewed 1857 times ]
So the rectangular figure has an approximate area of 60 - (16 - 4 pi ) = 56.566.
From here, we must subtract the area of the circle contained in the figure in order to determine the area of the shaded portion of the figure. As the figure is not drawn to scale, this will be a range of values.
Attachment:
GRE rectangle with a circle-1.jpg [ 11.74 KiB | Viewed 1907 times ]
As the radius of the circle is not specified, it could theoretically be an infinitesimally small. Take for example a circle with a radius of 0.01. The area of the circle would be: (0.01)^2 pi = 0.0003. Even this value subtracted from the area of the rectangular figure would be negligible. Thus, we can say that the Area Max = 56.566
To find the minimum area of the shaded portion of the figure, we set the area of the inner circle to it's maximum value:
Attachment:
Inner circle max.png [ 29.77 KiB | Viewed 1882 times ]
Subtracting this value from the area of the rectangular figure we can find the minimum area:
56.566 - 3 pi = 28.292 ----> Area min = 28.292
28.292 < QA < 56.566
QB = 30
As QB falls within QA's range, we can confirm that Answer Choice D is correct.
General Discussion
Re: The outer figure above is a rectangle with four rounded corn
[#permalink]
 22 Jul 2020, 22:56
22 Jul 2020, 22:56
1
OA is missing sir !





