
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
The scores for the 500 students who took Ms. Johnson’s fina
[#permalink]
 22 May 2017, 01:45
22 May 2017, 01:45
8
Expert Reply
31
Bookmarks
Question Stats:
 56% (02:34) correct
56% (02:34) correct
 43% (02:00) wrong
43% (02:00) wrong  based on 399 sessions
based on 399 sessions
Hide Show timer Statistics
The scores for the 500 students who took Ms. Johnson’s final exam have a normal distribution. There are 80 students who scored at least 92 points out of a possible 100 total points and 10 students who scored at or below 56.
Quantity A |
Quantity B |
The average (arithmetic mean) score on the final exam |
87 |
A) Quantity A is greater.
B) Quantity B is greater.
C) The two quantities are equal.
D) The relationship cannot be determined from the information given.
Re: The scores for the 500 students who took Ms. Johnson’s fina
[#permalink]
 18 Sep 2017, 09:57
18 Sep 2017, 09:57
8
Expert Reply
7
Bookmarks
OE
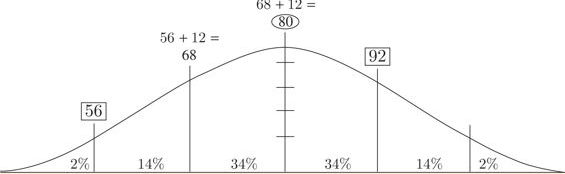
deviation.jpg [ 23.65 KiB | Viewed 30985 times ]
Attachment:
deviation.jpg [ 23.65 KiB | Viewed 30985 times ]
Quote:
Remember that a normal distribution curve has divisions of 34 percent, 14 percent, and 2 percent on each side of the mean. 80 out of 50 is 16 percent, or 14 percent + 2 percent, and 10 out of 500 is 2 percent. Draw a normal distribution curve and label it. There are three standard deviations between 92 and 56, so 92 - 56 = 36, and 36 ÷ 3 = 12. The mean is 92 - 12 = 80, which is smaller than Quantity B.
Retired Moderator
Joined: 10 Apr 2015
Posts: 6218
Given Kudos: 136
Re: The scores for the 500 students who took Ms. Johnson’s fina
[#permalink]
 26 May 2019, 13:18
26 May 2019, 13:18
9
1
Bookmarks
Carcass wrote:
The scores for the 500 students who took Ms. Johnson’s final exam have a normal distribution. There are 80 students who scored at least 92 points out of a possible 100 total points and 10 students who scored at or below 56.
Quantity A |
Quantity B |
The average (arithmetic mean) score on the final exam |
87 |
-------ASIDE-----------------------------
A little extra background on standard deviations above and below the mean
If, for example, a set has a standard deviation of 4, then:
1 standard deviation = 4
2 standard deviations = 8
3 standard deviations = 12
1.5 standard deviations = 6
0.25 standard deviations = 1
etc
So, if the mean of a set is 9, and the standard deviation is 4, then:
2 standard deviations ABOVE the mean = 17 [since 9 + 2(4) = 17]
1.5 standard deviations BELOW the mean = 3 [since 9 - 1.5(4) = 3]
3 standard deviations ABOVE the mean = 21 [since 9 + 3(4) = 21]
etc.
-------------------------------------------------
We're told that 16% scored at least 92 points (80/500 = 10%)
When we examine the normal distribution curve, we see that 16% of all values are more than 1 standard deviation ABOVE the mean.

So, we know that a test score of 92 points is 1 standard deviation ABOVE the mean.
So, if m = the mean of all the scores
and if d = the standard deviation of all the scores...
We can write: m + d = 92
We're also told that 2% scored less than 56 points (10/500 = 2%)
When we examine the normal distribution curve, we see that 2% of all values are more than 2 standard deviations BELOW the mean.

So, we know that a test score of 56 points is 2 standard deviations BELOW the mean.
So, if m = the mean of all the scores
and if d = the standard deviation of all the scores...
We can write: m - 2d = 56
So, we now know two things:
m + d = 92
m - 2d = 56
Take the TOP equation, and multiply both sides by 2 to get:
2m + 2d = 184
m - 2d = 56
ADD the two equations to get: 3m = 240
Solve: m = 80
Answer: 80
Cheers,
Brent









