
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
The side of a square ABCD measures 1 unit. Point E on side AB is such
[#permalink]
 18 Dec 2023, 01:11
18 Dec 2023, 01:11
Expert Reply
3
Bookmarks
Question Stats:
 33% (01:52) correct
33% (01:52) correct
 66% (02:39) wrong
66% (02:39) wrong  based on 12 sessions
based on 12 sessions
Hide Show timer Statistics
The side of a square ABCD measures 1 unit. Point E on side AB is such that, when the square is folded along the line DE, side AD coincides with diagonal BD.
A) Quantity A is greater.
B) Quantity B is greater.
C) The two quantities are equal.
D) The relationship cannot be determined from the information given.
Quantity A |
Quantity B |
The length of AE |
0.5 |
A) Quantity A is greater.
B) Quantity B is greater.
C) The two quantities are equal.
D) The relationship cannot be determined from the information given.
Part of the project: The Butler-GRE Daily New Quant and Verbal Questions to Practice (2023) - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
Re: The side of a square ABCD measures 1 unit. Point E on side AB is such
[#permalink]
 13 Jan 2024, 06:20
13 Jan 2024, 06:20
1
Expert Reply
Post A Detailed Correct Solution For these FRESH Quant & Verbal Questions And Get A Kudos
Re: The side of a square ABCD measures 1 unit. Point E on side AB is such
[#permalink]
 05 Mar 2024, 08:15
05 Mar 2024, 08:15
1
Expert Reply
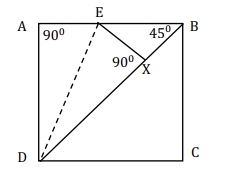
Let us focus on triangle ADB.
We know that DE is the internal angle bisector of ∠ADB.
In any equilateral triangle, the angle bisector also bisects the side opposite to the angle
it bisects.
Also, in an isosceles triangle, the angle bisector of the ‘unequal angle’ also bisects the
side opposite to that angle, i.e. it bisects the ‘unequal side’.
In this case, though triangle ADB is isosceles, the angle bisector bisects one of the equal angles
(since ∠ADB = ∠ABD = 45◦).
Thus, the angle bisector in this case, i.e. DE, does not bisect the side opposite to the
concerned angle.
Thus, DE does not bisect AB
=> AE 6= BE
Let us draw EX perpendicular to BD.
GRE square geometry.jpg [ 13.89 KiB | Viewed 1592 times ]
It is clear that triangles ADE and XDE are congruent to one another, since
DE is a common side, ∠DAE =∠DXE = 90◦, and ∠ADE =∠XDE
Thus, AE = EX.
In triangle EXB, EB is the hypotenuse, and hence, the longest side.
Thus, we have
EB > EX
=> EB > AE
Thus, AE must be less than half of AB
=> AE < 0.5
We know that DE is the internal angle bisector of ∠ADB.
In any equilateral triangle, the angle bisector also bisects the side opposite to the angle
it bisects.
Also, in an isosceles triangle, the angle bisector of the ‘unequal angle’ also bisects the
side opposite to that angle, i.e. it bisects the ‘unequal side’.
In this case, though triangle ADB is isosceles, the angle bisector bisects one of the equal angles
(since ∠ADB = ∠ABD = 45◦).
Thus, the angle bisector in this case, i.e. DE, does not bisect the side opposite to the
concerned angle.
Thus, DE does not bisect AB
=> AE 6= BE
Let us draw EX perpendicular to BD.
Attachment:
GRE square geometry.jpg [ 13.89 KiB | Viewed 1592 times ]
It is clear that triangles ADE and XDE are congruent to one another, since
DE is a common side, ∠DAE =∠DXE = 90◦, and ∠ADE =∠XDE
Thus, AE = EX.
In triangle EXB, EB is the hypotenuse, and hence, the longest side.
Thus, we have
EB > EX
=> EB > AE
Thus, AE must be less than half of AB
=> AE < 0.5




