GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Two circles with radious R & r intersect at 2 points. If R > r, then w
[#permalink]
10 May 2023, 05:05
10 May 2023, 05:05
Expert Reply
1
Bookmarks
00:00
Question Stats:
38% (00:54) correct
61% (01:25) wrong based on 13 sessions
Hide Show timer Statistics
Two circles with radious R & r intersect at 2 points. If R > r, then which of the following must be true?
Indicate all that apply
The distance between their centres is the sum of their radii
They have two common tangents
They can have only one common chord
Post A Detailed Correct Solution For The Above Questions And Get Kudos.
Question From Our Project: Free GRE Prep Club Tests in Exchange for 20 Kudos
\(\Longrightarrow\) GRE - Quant Daily Topic-wise Challenge
\(\Longrightarrow\) GRE GEOMETRY
Indicate all that apply
The distance between their centres is the sum of their radii
They have two common tangents
They can have only one common chord
Post A Detailed Correct Solution For The Above Questions And Get Kudos.
Question From Our Project: Free GRE Prep Club Tests in Exchange for 20 Kudos
\(\Longrightarrow\) GRE - Quant Daily Topic-wise Challenge
\(\Longrightarrow\) GRE GEOMETRY
Re: Two circles with radious R & r intersect at 2 points. If R > r, then w
[#permalink]
27 May 2023, 09:19
27 May 2023, 09:19
Expert Reply
OE
Given that, two circles with radius R and r intersect at two points. For R > r, let us check
which of the given statements are true.
A).
Given that, the distance between their centers is sum of their radii (R + r).
Case I
Consider circles intersecting at two points.
GRe circle (16).jpg [ 26.34 KiB | Viewed 1499 times ]
Here as both radii share some common part, distance between centers of both the circles is less than summation of radii.
Case II
Consider a case, where both circles intersect at only one point.
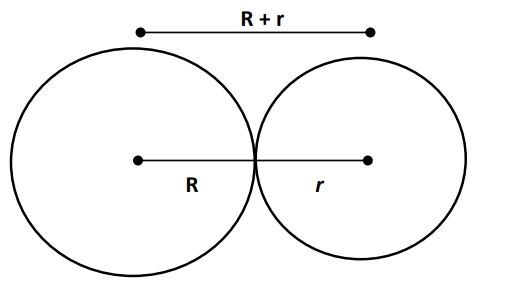
GRE circle2.jpg [ 27.96 KiB | Viewed 1520 times ]
In this case we can say, distance between center of both the circles is equal to the
summation of radii (R + r).
Hence, Statement A does not hold true for the possibility when two circles intersect at 2
points.
B).
Consider circles intersecting at two points.
We can draw exact two tangents common to these circles.
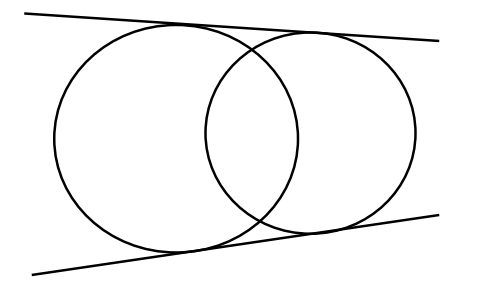
GRE circle 3.jpg [ 26.98 KiB | Viewed 1509 times ]
Hence, Statement B holds tru
C).
A segment joining any two points on a circle is a chord. For circles intersecting at 2
points, we can draw exactly one chord in common by joining the 2 points of
intersection.
Consider following figure.
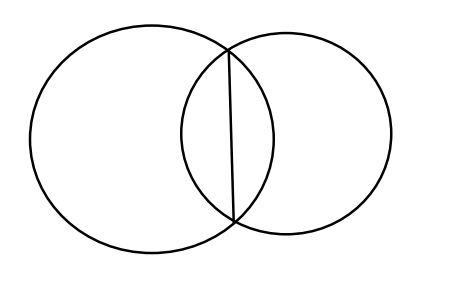
GRE circle 4.jpg [ 22.49 KiB | Viewed 1497 times ]
Hence statement C also holds true
Ans. (B, C)
Given that, two circles with radius R and r intersect at two points. For R > r, let us check
which of the given statements are true.
A).
Given that, the distance between their centers is sum of their radii (R + r).
Case I
Consider circles intersecting at two points.
Attachment:
GRe circle (16).jpg [ 26.34 KiB | Viewed 1499 times ]
Here as both radii share some common part, distance between centers of both the circles is less than summation of radii.
Case II
Consider a case, where both circles intersect at only one point.
Attachment:
GRE circle2.jpg [ 27.96 KiB | Viewed 1520 times ]
In this case we can say, distance between center of both the circles is equal to the
summation of radii (R + r).
Hence, Statement A does not hold true for the possibility when two circles intersect at 2
points.
B).
Consider circles intersecting at two points.
We can draw exact two tangents common to these circles.
Attachment:
GRE circle 3.jpg [ 26.98 KiB | Viewed 1509 times ]
Hence, Statement B holds tru
C).
A segment joining any two points on a circle is a chord. For circles intersecting at 2
points, we can draw exactly one chord in common by joining the 2 points of
intersection.
Consider following figure.
Attachment:
GRE circle 4.jpg [ 22.49 KiB | Viewed 1497 times ]
Hence statement C also holds true
Ans. (B, C)
gmatclubot
Re: Two circles with radious R & r intersect at 2 points. If R > r, then w [#permalink]
27 May 2023, 09:19
Moderators:
