GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Two interior angles of a convex quadrilateral ABCD are right angles (a
[#permalink]
08 Jan 2024, 00:03
08 Jan 2024, 00:03
Expert Reply
1
Bookmarks
00:00
Question Stats:
11% (01:30) correct
88% (02:54) wrong based on 9 sessions
Hide Show timer Statistics
Two interior angles of a convex quadrilateral ABCD are right angles (all interior angles are less than 180◦ and the two diagonals both lie inside the quadrilateral). The degree measure of ∠ABC is twice the degree measure of ∠BCD.
A) Quantity A is greater.
B) Quantity B is greater.
C) The two quantities are equal.
D) The relationship cannot be determined from the information given.
Quantity A |
Quantity B |
Measure of the largest interior angle of quadrilateral ABCD |
120° |
A) Quantity A is greater.
B) Quantity B is greater.
C) The two quantities are equal.
D) The relationship cannot be determined from the information given.
Part of the project: The Butler-GRE Daily New Quant and Verbal Questions to Practice (2023) - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
Manager
Joined: 11 Nov 2023
Posts: 207
Given Kudos: 76
WE:Business Development (Advertising and PR)
Two interior angles of a convex quadrilateral ABCD are right angles (a
[#permalink]
Updated on: 10 Jan 2024, 09:26
Updated on: 10 Jan 2024, 09:26
1
The sum of the interior angles of ALL quadrilaterals is 360°.
Given that 2 of the angles are 90° and 2 are not (since one will be twice the measure of the other), it's a trapezoid that looks something like this:
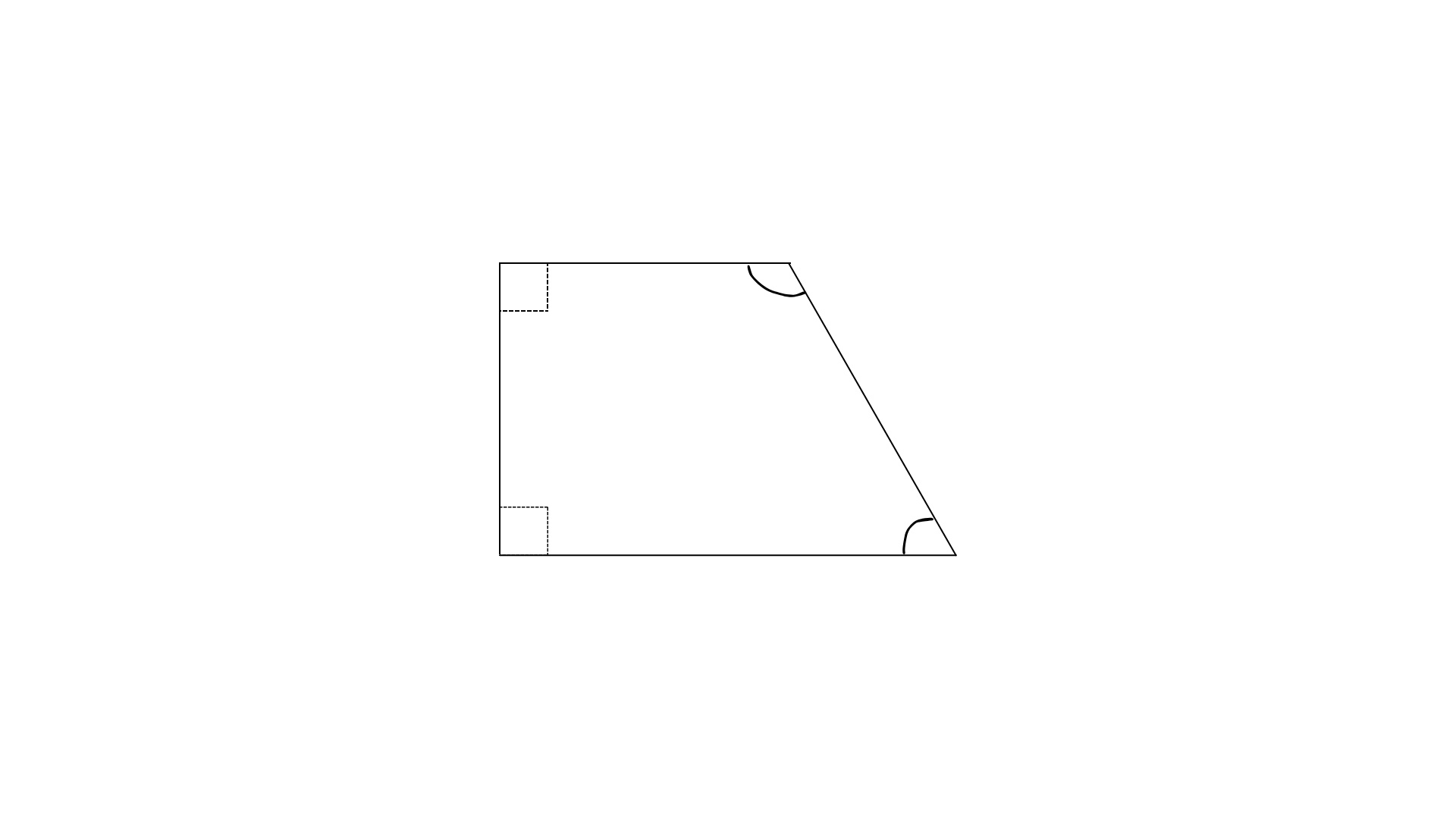
quad0.jpg [ 47.19 KiB | Viewed 664 times ]
where the 2 right angles are adjacent to each other. (The right angles can't be opposite to each other because that would make it a rectangle with all 4 angles being 90°) We also find that the 2 angles must be supplementary (add up to 180°) since 360 - (2*90) = 180.
However, the catch is that we don't know which angles correspond to ∠ABC and ∠BCD. There's 2 possible ways:
(1) 
quad1.jpg [ 33.3 KiB | Viewed 682 times ]
, (2)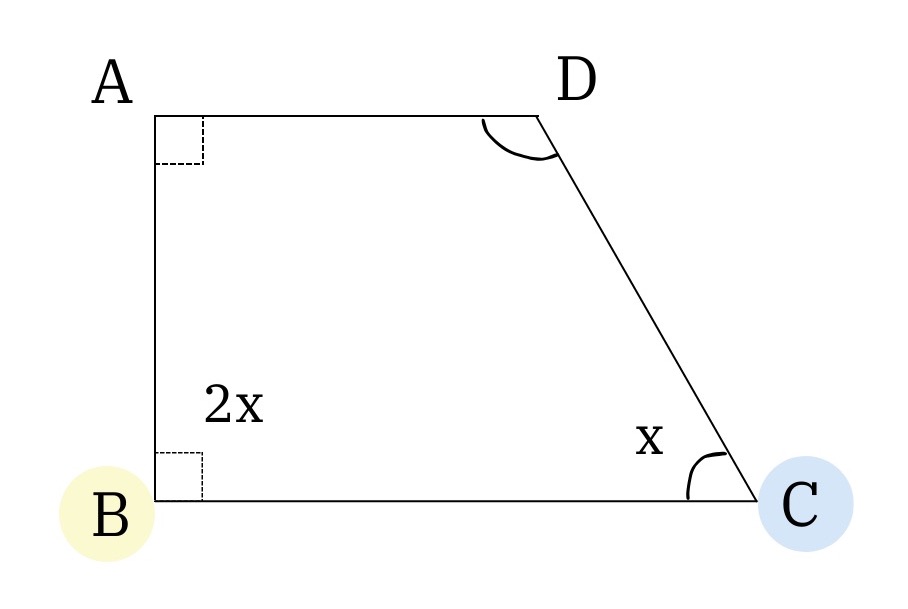 
quad2.jpg [ 29.04 KiB | Viewed 673 times ]
With (1), we'd previously found that the 2 non-right angles are supplementary, so 2x + x = 180 --> x = 60°. Since ∠ABC = 2x here, ∠ABC = 120°. The largest angle here is less than Quantity A.
With (2), ∠ABC = 90° = 2x ---> x = 45°. The 2 non-right angles are supplementary, so ∠CDA = 180 - 45 = 135°. The largest angle here is greater than Quantity B.
Since the largest angle could either be less than OR greater than Quantity B, the answer is D.
Given that 2 of the angles are 90° and 2 are not (since one will be twice the measure of the other), it's a trapezoid that looks something like this:
Attachment:
quad0.jpg [ 47.19 KiB | Viewed 664 times ]
where the 2 right angles are adjacent to each other. (The right angles can't be opposite to each other because that would make it a rectangle with all 4 angles being 90°) We also find that the 2 angles must be supplementary (add up to 180°) since 360 - (2*90) = 180.
However, the catch is that we don't know which angles correspond to ∠ABC and ∠BCD. There's 2 possible ways:
(1)
Attachment:
quad1.jpg [ 33.3 KiB | Viewed 682 times ]
Attachment:
quad2.jpg [ 29.04 KiB | Viewed 673 times ]
With (1), we'd previously found that the 2 non-right angles are supplementary, so 2x + x = 180 --> x = 60°. Since ∠ABC = 2x here, ∠ABC = 120°. The largest angle here is less than Quantity A.
With (2), ∠ABC = 90° = 2x ---> x = 45°. The 2 non-right angles are supplementary, so ∠CDA = 180 - 45 = 135°. The largest angle here is greater than Quantity B.
Since the largest angle could either be less than OR greater than Quantity B, the answer is D.
Originally posted by nurirachel on 10 Jan 2024, 09:09.
Last edited by nurirachel on 10 Jan 2024, 09:26, edited 2 times in total.
Last edited by nurirachel on 10 Jan 2024, 09:26, edited 2 times in total.
Re: Two interior angles of a convex quadrilateral ABCD are right angles (a
[#permalink]
10 Jan 2024, 09:18
10 Jan 2024, 09:18
Expert Reply
the images do not show up sir
