
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.

Question Stats:
 6% (01:24) correct
6% (01:24) correct
 93% (01:22) wrong
93% (01:22) wrong  based on 133 sessions
based on 133 sessions
Hide Show timer Statistics
I. 2
II. 12
III. 24
A. I only
B. I and II only
C. II and III only
D. I and III only
E. I, II, and III
Last edited by Carcass on 30 Dec 2022, 11:29, edited 7 times in total.
I. 2
II. 12
III. 24
Indicate all possible values
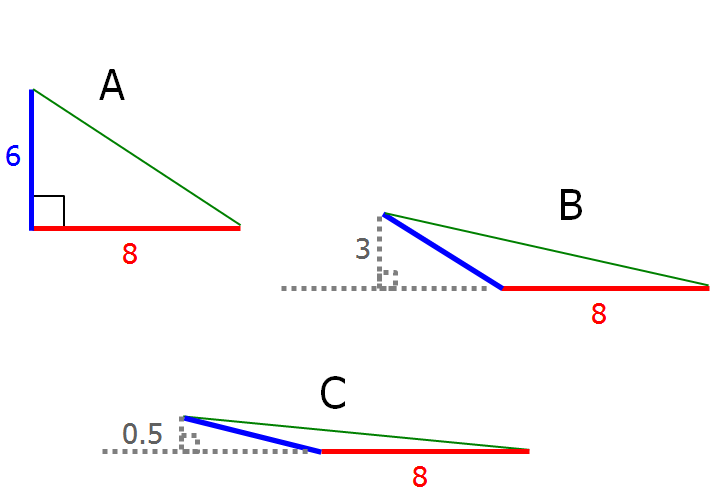
As we can see from the diagrams above, all 3 areas are possible.
Area = (base)(height)/2
The area of triangle A = (8)(6)/2 = 24
The area of triangle B = (8)(3)/2 = 12
The area of triangle C = (8)(0.5)/2 = 2
Once we prove that, by positioning the two lengths at right angles, we can create a triangle with area 24, we can rotate the side with length 6 so that the triangle's height gets smaller and smaller, which allows us to create triangles with area 12 and 2.
Answer: I, II and III
RELATED VIDEO
-. If you are given two sides of a triangle
. minimum area is practically 0
. maximum area is the area of right triangle formed by the two sides
. either side can be the base and the other side will be the height
-. Example
. Given triangle with sides of 6 and 8
.. minimum area = 0
.. maximum area = 24
.. therefore answer is A,B,C (or I, II, and III)
- Short Explanation:
-. Why?
. area is a function of height (1/2 base times height)
. height of a triangle is maximized when one of it’s angles is 90˚
. height is minimized when the angle is 0˚ or 180ˆ, at which point the area is basically 0
. so the range of area of any triangle formed from two given sides is at a minimum practically 0 and at a maximum the area of the right triangle formed by the two sides
See attached illustrations, or try out interactive triangle tool for yourself at: https://www.mathsisfun.com/geometry/pol ... ctive.html
- Long Explanation:
Basically here’s my thoughts on it
1) What is the maximum and minimum area possible? If we know that, then we can see if the answers are within that range
2) So, what’s the maximum area possible given the sides we were given?
. we know Area = 1/2 base times height
. but we don’t have height
. either 6 or 8 could be the base, but since we aren’t given any angles, we don’t know what the height is
. what possible height, given just these two sides, will give us maximum area?
. lets draw it out
. lets start with the lines basically flat
. what’s our height?
. it’s basically 0, maybe 0.0000000001
. so since our height is practically 0 our area would practically be 0
.. what if we start raising up the big side?
.. what happens to height?
.. we see it gets larger
.. as area is basically just the product of base and height we will have maximum area when we have maximum height
. so when will this happen?
. it’ll happen when the line is going straight up
. which is a 90 degree angle
. so then our area is 1/2 b • h = 1/2 6ª8 which is 24.
-. some might say, well, what about if our third side was the maximum possible, which is just the sum of six plus eight? Yes, then you would have a side of 14. But if you had that side, then the triangle would basically be flat
. and therefore your area would basically be 0.
-. so what about the opposite, what about when we have the rule for the third side which tells us the minimum length?
. well that would be slightly more than the difference which is 2. Well, if the third side is 2, what do we have? Again, you will basically have a closed triangle, which is flat.
. so the area would be practically 0
. so our maximum area, again, is when we have a right triangle because that’s when our height is the greatest. It doesn’t matter which side is the base, the result will be the same. You can tell just by looking at the formula, since we know we must use a right
triangle for maximum area then the base and the height in this case will just be the two given sides of the triangle, and they are interchangeable
- Note on attached illustrations
. I kept the base as 6 and the one side as 8
. I let the other side vary as I changed the angle between the base side of 6 and the 8 side
. if you look in the upper left corner you can see the area of the triangle and how it's maximized when the angle is 90˚
. and it's practically 0 when the angle is 0˚ or 180˚
Screen Shot 2019-08-28 at 11.47.51 PM.jpg [ 275.5 KiB | Viewed 21820 times ]
Screen Shot 2019-08-28 at 11.47.08 PM.jpg [ 276.44 KiB | Viewed 21827 times ]
Screen Shot 2019-08-28 at 11.46.53 PM.jpg [ 277.02 KiB | Viewed 21850 times ]
Screen Shot 2019-08-28 at 11.46.28 PM.jpg [ 277.53 KiB | Viewed 21845 times ]
Screen Shot 2019-08-28 at 11.46.20 PM.jpg [ 276.19 KiB | Viewed 21785 times ]
Screen Shot 2019-08-28 at 11.45.46 PM.jpg [ 276.61 KiB | Viewed 21838 times ]
Screen Shot 2019-08-28 at 11.45.20 PM.jpg [ 277.39 KiB | Viewed 21818 times ]
Screen Shot 2019-08-28 at 11.45.02 PM.jpg [ 277.34 KiB | Viewed 21793 times ]







