GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
O is the center of the circle and OS=SQ.
[#permalink]
15 Jul 2021, 05:59
15 Jul 2021, 05:59
Expert Reply
00:00
Question Stats:
42% (01:02) correct
57% (01:34) wrong based on 14 sessions
Hide Show timer Statistics
Attachment:
GRE O is the center of the circle and OS=SQ..jpg [ 10.26 KiB | Viewed 1310 times ]
O is the center of the circle and OS=SQ.
Quantity A |
Quantity B |
PQ |
OR |
A)The quantity in Column A is greater.
B)The quantity in Column B is greater.
C)The two quantities are equal.
D)The relationship cannot be determined from the information given.
Kudos for the right answer and explanation
Question part of the project GRE Quantitative Reasoning Daily Challenge - (2021) EDITION
GRE - Math Book
Moderator
Joined: 02 Jan 2020
Status:GRE Quant Tutor
Posts: 1111
Given Kudos: 9
Location: India
Concentration: General Management
Schools: XLRI Jamshedpur, India - Class of 2014
GMAT 1: 700 Q51 V31
GPA: 2.8
WE:Engineering (Computer Software)
O is the center of the circle and OS=SQ.
[#permalink]
15 Jul 2021, 08:15
15 Jul 2021, 08:15
1
Let's Join O and P as shown in the image below
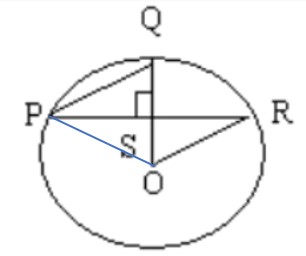
image.jpg [ 9.84 KiB | Viewed 1264 times ]
In \(\triangle\)POR
-> OP = OR = Radius
=> \(\triangle\)POR is an isosceles triangle.
\(\angle\)OSP = \(90^{\circ}\) [ As \(\angle\)PSQ= \(90^{\circ}\) ]
And we know that, in an Isosceles Triangle the perpendicular drawn from the vertex tot he non equal side, bisects the side
=> OS will bisect PR
=> PS = SR
Now, consider \(\triangle\)PSQ and \(\triangle\)RSO
PS = SR (proved above)
OS = OQ (given)
And the included angle, \(\angle\)PSQ = \(\angle\)RSO = \(90^{\circ}\)
=> \(\triangle\)PSQ ≅ \(\triangle\)RSO [Congruent triangles, all corresponding sides and all corresponding angles will be equal]
=> PQ = OR
=> Quantity A = Quantity B
So, answer will C
Hope it helps!
Watch the following video to Learn Basics of Circles
Attachment:
image.jpg [ 9.84 KiB | Viewed 1264 times ]
In \(\triangle\)POR
-> OP = OR = Radius
=> \(\triangle\)POR is an isosceles triangle.
\(\angle\)OSP = \(90^{\circ}\) [ As \(\angle\)PSQ= \(90^{\circ}\) ]
And we know that, in an Isosceles Triangle the perpendicular drawn from the vertex tot he non equal side, bisects the side
=> OS will bisect PR
=> PS = SR
Now, consider \(\triangle\)PSQ and \(\triangle\)RSO
PS = SR (proved above)
OS = OQ (given)
And the included angle, \(\angle\)PSQ = \(\angle\)RSO = \(90^{\circ}\)
=> \(\triangle\)PSQ ≅ \(\triangle\)RSO [Congruent triangles, all corresponding sides and all corresponding angles will be equal]
=> PQ = OR
=> Quantity A = Quantity B
So, answer will C
Hope it helps!
Watch the following video to Learn Basics of Circles
gmatclubot
O is the center of the circle and OS=SQ. [#permalink]
15 Jul 2021, 08:15
Moderators:
