GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
A square is inscribed inside a shaded circle, as shown. The
[#permalink]
09 Mar 2019, 12:27
09 Mar 2019, 12:27
Expert Reply
00:00
Question Stats:
80% (01:30) correct
19% (02:12) wrong based on 31 sessions
Hide Show timer Statistics
A square is inscribed inside a shaded circle, as shown. The circumference of the circle is \(6 \pi \sqrt{2}\). What is the area of the shaded region?
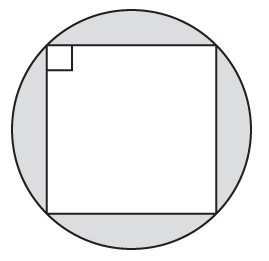
#GREpracticequestion A square is inscribed inside a shaded circle, as shown..jpg [ 14.78 KiB | Viewed 4149 times ]
A. \(12\pi - 6 \sqrt{2}\)
B. \(12\pi - 18\)
C. \(18\pi - 6\)
D. \(18\pi - 36\)
E. \(36\pi - 18\)
Attachment:
#GREpracticequestion A square is inscribed inside a shaded circle, as shown..jpg [ 14.78 KiB | Viewed 4149 times ]
A. \(12\pi - 6 \sqrt{2}\)
B. \(12\pi - 18\)
C. \(18\pi - 6\)
D. \(18\pi - 36\)
E. \(36\pi - 18\)
Re: A square is inscribed inside a shaded circle, as shown. The
[#permalink]
17 Mar 2019, 18:12
17 Mar 2019, 18:12
Expert Reply
The circumference of a circle is equal to \(2\pi r\). Hence:
\(2\pi r\) = \(6\pi \sqrt{2}\)
Divide by \(2\pi\):
\(r = 3\sqrt{2}\)
The area of the whole circle is \(\pi r^{2}\). So:
\(\pi (3\sqrt{2})^{2} = \pi 9(2) = 18\pi\)
At this point, I'm going to cheat. No need calculating more than we need to. Only C and D start with \(18\pi\), the full area of the circle. \(18\pi\) is somewhere near 54, and the square takes up at least half of that total area. In other words, we'll be subtracting more than 6. 36 is more like it, so D is the answer.
\(2\pi r\) = \(6\pi \sqrt{2}\)
Divide by \(2\pi\):
\(r = 3\sqrt{2}\)
The area of the whole circle is \(\pi r^{2}\). So:
\(\pi (3\sqrt{2})^{2} = \pi 9(2) = 18\pi\)
At this point, I'm going to cheat. No need calculating more than we need to. Only C and D start with \(18\pi\), the full area of the circle. \(18\pi\) is somewhere near 54, and the square takes up at least half of that total area. In other words, we'll be subtracting more than 6. 36 is more like it, so D is the answer.
gmatclubot
Re: A square is inscribed inside a shaded circle, as shown. The [#permalink]
17 Mar 2019, 18:12
Moderators:
