GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
In the figure below, square ABCD is inscribed in circle O. I
[#permalink]
02 Feb 2019, 02:27
02 Feb 2019, 02:27
Expert Reply
00:00
Question Stats:
78% (01:33) correct
21% (01:22) wrong based on 76 sessions
Hide Show timer Statistics
In the figure below, square ABCD is inscribed in circle O. If the perimeter of ABCD is 24, what is the area of the shaded region?
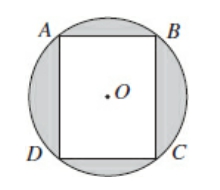
#GREpracticequestion In the figure below, square ABCD.jpg [ 13.34 KiB | Viewed 8497 times ]
A) \(18 \pi - 36\)
B) \(18 \pi - 24\)
C) \(12 \pi - 36\)
D) \(9 \pi - 36\)
E) \(9 \pi - 24\)
Attachment:
#GREpracticequestion In the figure below, square ABCD.jpg [ 13.34 KiB | Viewed 8497 times ]
A) \(18 \pi - 36\)
B) \(18 \pi - 24\)
C) \(12 \pi - 36\)
D) \(9 \pi - 36\)
E) \(9 \pi - 24\)
Re: In the figure below, square ABCD is inscribed in circle O. I
[#permalink]
02 Feb 2019, 04:15
02 Feb 2019, 04:15
3
Carcass wrote:
In the figure below, square ABCD is inscribed in circle O. If the perimeter of ABCD is 24, what is the area of the shaded region?
A) \(18 \pi - 36\)
B) \(18 \pi - 24\)
C) \(12 \pi - 36\)
D) \(9 \pi - 36\)
E) \(9 \pi - 24\)
Attachment:
#GREpracticequestion In the figure below, square ABCD.jpg
A) \(18 \pi - 36\)
B) \(18 \pi - 24\)
C) \(12 \pi - 36\)
D) \(9 \pi - 36\)
E) \(9 \pi - 24\)
Explanation::
Perimeter of the square = 24
i.e. 4*Side of square = 24
or side of the square = 6
Area of square = \(6^2 = 36\)
Now Area of square = \(\frac{{diagonal}^2}{2}\)
or \(36 * 2 = diagonal^2\)
or diagonal = diameter of the circle = \(6\sqrt{2}\)
Area of the circle = \(\pi * radius^2 = \pi * (3\sqrt{2})^2 = 18\pi\)
Required area = Area of circle - Area of square
= \(18\pi − 36\)
Re: In the figure below, square ABCD is inscribed in circle O. I
[#permalink]
04 Jan 2022, 21:43
04 Jan 2022, 21:43
Hello from the GRE Prep Club BumpBot!
Thanks to another GRE Prep Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).
Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.
Thanks to another GRE Prep Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).
Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.
