GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
In the above figure, if $A D=3$, what is the perimeter of triangle $A
[#permalink]
03 Feb 2025, 01:00
03 Feb 2025, 01:00
Expert Reply
00:00
Question Stats:
100% (01:27) correct
0% (00:00) wrong based on 6 sessions
Hide Show timer Statistics
Attachment:
GRE In the above figure, if AD = 3.png [ 36.01 KiB | Viewed 146 times ]
In the above figure, if $\(A D=3\)$, what is the perimeter of triangle $\(A B C\)$ ?
(A) \(12\)
(B) \(13\)
(C) $\(9+\sqrt{3}\)$
(D) $\(9+\sqrt{27}\)$.
(E) \(15\)
- Part of the project: GRE Quant & Verbal ADVANCED Daily Challenge 2024 Edition - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
- Also replying to the unanswered questions
Re: In the above figure, if $A D=3$, what is the perimeter of triangle $A
[#permalink]
06 Mar 2025, 11:05
06 Mar 2025, 11:05
Expert Reply
A triangle having angles 30, 60 \& 90 , the corresponding opposite sides are $\(\mathrm{a}, \mathrm{a} \sqrt{3} \& 2 \mathrm{a}\)$ respectively. Similarly the right triangle having angles $\(90,45 \& 45\)$, the corresponding opposite sides are $\(\mathrm{a} \sqrt{2}\)$, a \& a respectively.
GRE triangle triplete.png [ 41.93 KiB | Viewed 54 times ]
Using the above two right triangle rules we can find the remaining sides in the given figure.
In triangle ADC , the side opposite to 45 degree is $\(\mathrm{x}=\mathrm{AD}\)$, so the side AC would also be x Next in triangle ABC , angles are $90,60 \& 30$, where the side opposite to 30 is $\(\mathrm{AC}=\mathrm{x}\)$, so the remaining sides opposite to $\(60 \& 90\)$ would be $\(\mathrm{x} \sqrt{3}(=\mathrm{BA}) \& 2 \mathrm{x}(=\mathrm{BC})\)$ respectively.
The sides when mentioned in the figure we get
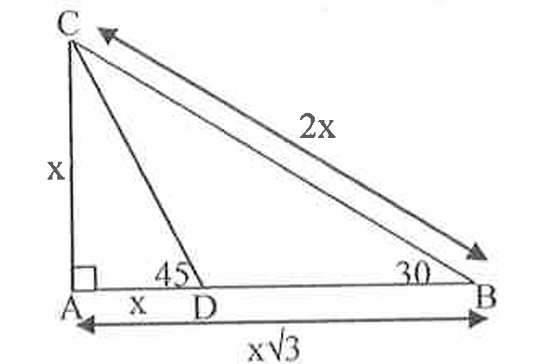
GRE triangle sides.png [ 78.73 KiB | Viewed 54 times ]
Hence the perimeter of the triangle $\(A B C\)$ is $\(x+x \sqrt{3}+2 x=3 x+x \sqrt{3}\)$, which for $\(A D=3(=x)\)$ comes out to be $\(9+\sqrt{27}\)$, so the answer is (D).
Attachment:
GRE triangle triplete.png [ 41.93 KiB | Viewed 54 times ]
Using the above two right triangle rules we can find the remaining sides in the given figure.
In triangle ADC , the side opposite to 45 degree is $\(\mathrm{x}=\mathrm{AD}\)$, so the side AC would also be x Next in triangle ABC , angles are $90,60 \& 30$, where the side opposite to 30 is $\(\mathrm{AC}=\mathrm{x}\)$, so the remaining sides opposite to $\(60 \& 90\)$ would be $\(\mathrm{x} \sqrt{3}(=\mathrm{BA}) \& 2 \mathrm{x}(=\mathrm{BC})\)$ respectively.
The sides when mentioned in the figure we get
Attachment:
GRE triangle sides.png [ 78.73 KiB | Viewed 54 times ]
Hence the perimeter of the triangle $\(A B C\)$ is $\(x+x \sqrt{3}+2 x=3 x+x \sqrt{3}\)$, which for $\(A D=3(=x)\)$ comes out to be $\(9+\sqrt{27}\)$, so the answer is (D).
gmatclubot
Re: In the above figure, if $A D=3$, what is the perimeter of triangle $A [#permalink]
06 Mar 2025, 11:05
Moderators:
