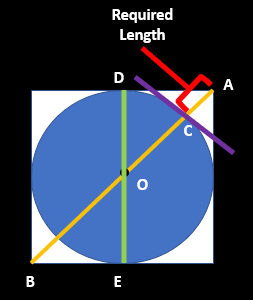
Given that A sphere is inscribed in a cube with an edge of 10. And we need to find What is the shortest possible distance from one of the vertices of the cube to the surface of the sphereShortest distance between any two points is achieved by dropping a perpendicular from one point to another.To find the Shortest distance between the vertex of the cube (Refer point A in the below image) and the surface of the sphere (Refer point C), we need to drop a perpendicular from A to the surface of the sphere.
Attachment:
 cube sphere.png [ 12.91 KiB | Viewed 5145 times ]
cube sphere.png [ 12.91 KiB | Viewed 5145 times ]
We know that the diagonals of a cube are Perpendicular bisectors of each other => The perpendicular from A to the surface of C will pass through O (the center of the cube and the sphere)
=> Distance AC = AO - CO = \(\frac{1}{2}\) * (Diagonal of cube) - \(\frac{1}{2}\) * (Diagonal of Sphere)
We know that Side of Cube = 10, and Diagonal of Cube = \(\sqrt{3}\) * Side = \(\sqrt{3}\) * 10
Since, sphere is touching the cube so if we look at the vertical diameter(DE) of the sphere then it will be same as the side of the cube = 10
=> Distance AC = \(\frac{1}{2}\) * (Diagonal of cube) - \(\frac{1}{2}\) * (Diagonal of Sphere) = \(\frac{1}{2}\) * (\(\sqrt{3}\) * 10 - 10) = \(5(\sqrt{3} – 1)\)
So,
Answer will be BHope it helps!








 48% (02:01) correct
48% (02:01) correct




