
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
A flagpole stands perpendicular to the ground. At noon, the flagpole c
[#permalink]
 09 Aug 2022, 07:42
09 Aug 2022, 07:42
Expert Reply
3
Bookmarks
Question Stats:
 99% (01:21) correct
99% (01:21) correct
 0% (00:00) wrong
0% (00:00) wrong  based on 14 sessions
based on 14 sessions
Hide Show timer Statistics
A flagpole stands perpendicular to the ground. At noon, the flagpole casts a shadow on the ground that is 6 feet long. At the same time, a 5 foot tall woman stands next to the flagpole and casts a shadow that is 3 feet long. The woman is also perpendicular to the ground. Assume that the triangles created in both situations are similar.
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Quantity A |
Quantity B |
the height of the flagpole |
9 feet |
A. Quantity A is greater
B. Quantity B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
Part of the project: GRE Quantitative Comparison GEOMETRY+Tricky Questions - Special Summer Edition (2022)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
GRE Math Essentials (2022)
GRE Geometry Formulas
GRE - Math Book
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
GRE Math Essentials (2022)
GRE Geometry Formulas
GRE - Math Book
A flagpole stands perpendicular to the ground. At noon, the flagpole c
[#permalink]
 21 Aug 2022, 02:59
21 Aug 2022, 02:59
Expert Reply
OE
Quote:
Drawing a diagram may be helpful to solving this problem.
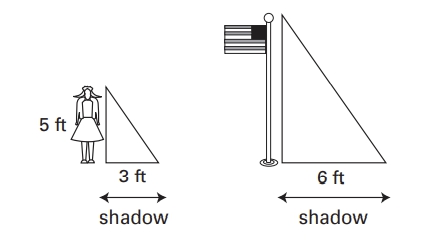
GRE Drawing a diagram may be helpful to solving this problem..jpg [ 22.4 KiB | Viewed 3058 times ]
The relationships between the flagpole and its shadow and the
woman and her shadow can be depicted as a right triangles
because both the flagpole and the woman are perpendicular to
the ground. The problem states that the triangles are similar.
Similar triangles have sides of lengths proportionate to each
other, so a ratio can be set up between the ratio of the flagpole’s
height to the length of its shadow and the woman’s height to
the length of her shadow as such, where x represents the height
of the flagpole in feet:
\(\frac{x}{lenth of shadow}=\frac{height of woman}{length of shadow}\)
\(\frac{x}{6}=\frac{5}{3}\)
\(3x=30\)
\(x=10 \)
The flagpole is 10 feet tall, which is greater than the value in
column B. Therefore the answer is a.
Attachment:
GRE Drawing a diagram may be helpful to solving this problem..jpg [ 22.4 KiB | Viewed 3058 times ]
The relationships between the flagpole and its shadow and the
woman and her shadow can be depicted as a right triangles
because both the flagpole and the woman are perpendicular to
the ground. The problem states that the triangles are similar.
Similar triangles have sides of lengths proportionate to each
other, so a ratio can be set up between the ratio of the flagpole’s
height to the length of its shadow and the woman’s height to
the length of her shadow as such, where x represents the height
of the flagpole in feet:
\(\frac{x}{lenth of shadow}=\frac{height of woman}{length of shadow}\)
\(\frac{x}{6}=\frac{5}{3}\)
\(3x=30\)
\(x=10 \)
The flagpole is 10 feet tall, which is greater than the value in
column B. Therefore the answer is a.
Re: A flagpole stands perpendicular to the ground. At noon, the flagpole c
[#permalink]
 21 Aug 2022, 03:03
21 Aug 2022, 03:03
Expert Reply




