GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
A square is formed by joining midpoints of another square. Perimeter
[#permalink]
12 Jan 2025, 23:30
12 Jan 2025, 23:30
Expert Reply
00:00
Question Stats:
33% (01:38) correct
66% (01:08) wrong based on 3 sessions
Hide Show timer Statistics
A square is formed by joining midpoints of another square. Perimeter of the larger square is X.
Quantity A |
Quantity B |
Perimeter of smaller square |
\(\frac{ X}{2}\) |
- Part of the project: GRE Quant & Verbal ADVANCED Daily Challenge 2024 Edition - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
- Also replying to the unanswered questions
A square is formed by joining midpoints of another square. Perimeter
[#permalink]
22 Feb 2025, 01:00
22 Feb 2025, 01:00
Expert Reply
OFFICIAL EXPLANATION
\(\text { Let } \mathrm{ABCD} \text { be the square whose midpoints are joined to form another square say } \mathrm{PQRS}\)
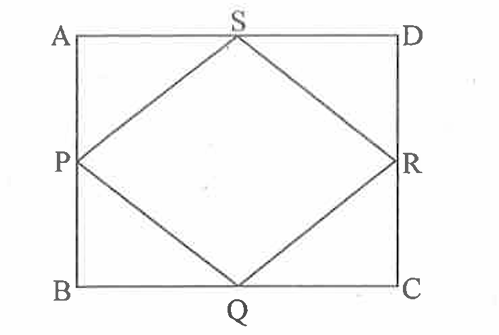
GRE ABCD.png [ 47.93 KiB | Viewed 11 times ]
We know that the perimeter of the larger square i.e. $\(A B C D\)$ is $x$, so we get side of the square ABCD as $\(\frac{X}{4}\)$ each (Perimeter of square is $\(=4 \times$ Side )\).
Using Pythagoras theorem i.e. Hypotenuse $\({ }^2=\)$ Perpendicular $\(^2+\)$ Base $\(^2\)$ in triangle APS, we get
$\(\mathrm{PS}=\sqrt{AP^2+AS^2}=\sqrt{ (\frac{x}{8})^2+(\frac{x}{8})^2}=\frac{x \sqrt{2}}{8}\)$ (The length of $\(\mathrm{AS}=\mathrm{AP}=\)$ half of the $\mathrm{AB}=\frac{x}{4}[/m]$ ).
So, the perimeter of the smaller square i.e. $\(\mathrm{PQRS}=4 \times \operatorname{Side}\)\(=4 \times \frac{x\sqrt{2}}{8}=\frac{x\sqrt{2}}{2}=\frac{x}{\sqrt{2}}\)$ Column A quantity) which is clearly greater than $\(\frac{x}{2}\)$ (= column B quantity).
Hence the answer is (A).
\(\text { Let } \mathrm{ABCD} \text { be the square whose midpoints are joined to form another square say } \mathrm{PQRS}\)
Attachment:
GRE ABCD.png [ 47.93 KiB | Viewed 11 times ]
We know that the perimeter of the larger square i.e. $\(A B C D\)$ is $x$, so we get side of the square ABCD as $\(\frac{X}{4}\)$ each (Perimeter of square is $\(=4 \times$ Side )\).
Using Pythagoras theorem i.e. Hypotenuse $\({ }^2=\)$ Perpendicular $\(^2+\)$ Base $\(^2\)$ in triangle APS, we get
$\(\mathrm{PS}=\sqrt{AP^2+AS^2}=\sqrt{ (\frac{x}{8})^2+(\frac{x}{8})^2}=\frac{x \sqrt{2}}{8}\)$ (The length of $\(\mathrm{AS}=\mathrm{AP}=\)$ half of the $\mathrm{AB}=\frac{x}{4}[/m]$ ).
So, the perimeter of the smaller square i.e. $\(\mathrm{PQRS}=4 \times \operatorname{Side}\)\(=4 \times \frac{x\sqrt{2}}{8}=\frac{x\sqrt{2}}{2}=\frac{x}{\sqrt{2}}\)$ Column A quantity) which is clearly greater than $\(\frac{x}{2}\)$ (= column B quantity).
Hence the answer is (A).
gmatclubot
A square is formed by joining midpoints of another square. Perimeter [#permalink]
22 Feb 2025, 01:00
Moderators:
