
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
All the arcs inscribed in the square
[#permalink]
 20 Mar 2024, 07:58
20 Mar 2024, 07:58
Expert Reply
2
Bookmarks
Question Stats:
 57% (02:20) correct
57% (02:20) correct
 42% (01:12) wrong
42% (01:12) wrong  based on 35 sessions
based on 35 sessions
Hide Show timer Statistics
All the arcs inscribed in the square have equal radii. Each of the arcs touches its neighbor at exactly one point.
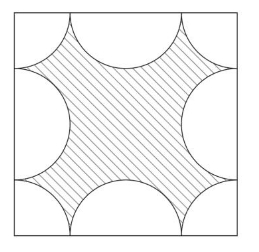
GRe arcs.jpg [ 31.5 KiB | Viewed 2094 times ]
A) Quantity A is greater.
B) Quantity B is greater.
C) The two quantities are equal.
D) The relationship cannot be determined from the information given.
Attachment:
GRe arcs.jpg [ 31.5 KiB | Viewed 2094 times ]
Quantity A |
Quantity B |
The area of the shaded region |
The area of the UNshaded region |
A) Quantity A is greater.
B) Quantity B is greater.
C) The two quantities are equal.
D) The relationship cannot be determined from the information given.
Part of the project: The Butler-GRE Daily New Quant and Verbal Questions to Practice (2023) - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Free Materials for the GRE General Exam - Where to get it!!
GRE Geometry Formulas
GRE - Math Book
Re: All the arcs inscribed in the square
[#permalink]
 27 May 2024, 15:45
27 May 2024, 15:45
1
using algebra here could get ugly, so I'll choose numbers. Let say our square has a side length of 12, this means that the radius of the circles is 3. We have 4 semi circles and 4 quarter of circles. Now that we have all our information we can solve the problem.
The area of the circle is=144
The area of the semi of 4 semi circles= 4(9pi/2)=2(9pi)
The area of the 4 quarter of circles is= 4(9pi/4)= 9pi
We add those like (2x+x=3x) it would be 3(9pi)
Now subtract 144-3(9pi)= 84.78 (area of the unshaded region)
The are of the shaded region is 144-84.78=59.22
Hence the correct answer is B
The area of the circle is=144
The area of the semi of 4 semi circles= 4(9pi/2)=2(9pi)
The area of the 4 quarter of circles is= 4(9pi/4)= 9pi
We add those like (2x+x=3x) it would be 3(9pi)
Now subtract 144-3(9pi)= 84.78 (area of the unshaded region)
The are of the shaded region is 144-84.78=59.22
Hence the correct answer is B
Re: All the arcs inscribed in the square
[#permalink]
 25 Sep 2024, 18:08
25 Sep 2024, 18:08
1
With a simple trick, the algebraic solution isn't so bad. Let r be the radius of each semi-circle and quarter-circle.
One side of the square = 4r, so the area of the square = 16(r^2).
For the unshaded area, notice that the 4 semi-circles make two full circles,
and the 4-quarter circles make 1 full circle for a total of 3 circles worth of area.
The area of one circle is (π)(r^2), so the unshaded area = 3π(r^2).
To find the shaded area we subtract the unshaded area from the total area of the square.
This will equal 16(r^2) - 3π(r^2) and we want to compare this to 3π(r^2).
We can divide by r^2 and add 3π to each expression leaving us with 16 (shaded region) and 6π (unshaded region). 6π ≈ 6(3.14) > 16.
So the unshaded region is larger than the shaded region and the answer is B.
You may also notice that (1/2)(16) = 8 and 3π > 8,
meaning the unshaded region's area takes up more than half of the total area of the square and is therefore larger than the shaded region.
One side of the square = 4r, so the area of the square = 16(r^2).
For the unshaded area, notice that the 4 semi-circles make two full circles,
and the 4-quarter circles make 1 full circle for a total of 3 circles worth of area.
The area of one circle is (π)(r^2), so the unshaded area = 3π(r^2).
To find the shaded area we subtract the unshaded area from the total area of the square.
This will equal 16(r^2) - 3π(r^2) and we want to compare this to 3π(r^2).
We can divide by r^2 and add 3π to each expression leaving us with 16 (shaded region) and 6π (unshaded region). 6π ≈ 6(3.14) > 16.
So the unshaded region is larger than the shaded region and the answer is B.
You may also notice that (1/2)(16) = 8 and 3π > 8,
meaning the unshaded region's area takes up more than half of the total area of the square and is therefore larger than the shaded region.






