
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Each side of the square ABCD shown below is 10. What is the area of t
[#permalink]
 14 Feb 2025, 01:27
14 Feb 2025, 01:27
Expert Reply
Question Stats:
 70% (01:31) correct
70% (01:31) correct
 29% (02:32) wrong
29% (02:32) wrong  based on 17 sessions
based on 17 sessions
Hide Show timer Statistics
Each side of the square ABCD shown below is 10. What is the area of the shaded region, if E and F are mid-points of the sides AD and BD respectively?
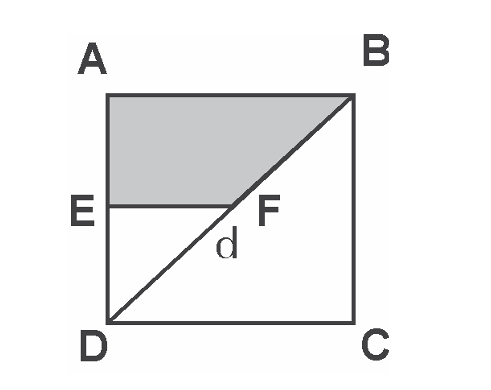
GRE suqare shade part.png [ 14.24 KiB | Viewed 857 times ]
(A) 75
(B) 37.5
(C) 25
(D) 18.75
(E) 15
Attachment:
GRE suqare shade part.png [ 14.24 KiB | Viewed 857 times ]
(A) 75
(B) 37.5
(C) 25
(D) 18.75
(E) 15
- Part of the project: GRE Quant & Verbal ADVANCED Daily Challenge 2025 NEW Edition - Gain 20 Kudos & Get FREE Access to GRE Prep Club TESTS
- Also replying to the unanswered questions
Re: Each side of the square ABCD shown below is 10. What is the area of t
[#permalink]
 08 Mar 2025, 10:53
08 Mar 2025, 10:53
Expert Reply
Attachment:
GRE square (2).png [ 65.53 KiB | Viewed 766 times ]
In the square ABCD above, each side is 10 , so the area of half of the square i.e. area of triangle $\(A B C=\frac{1}{2}(\text { Side })^2=\frac{1}{2}(10)^2=50\)$
As $\(\mathrm{E} \& \mathrm{~F}\)$ are the midpoints of $\(\mathrm{AC} \& \mathrm{BC}\)$ respectively, so we get $\(\mathrm{EF}=\frac{1}{2}(\mathrm{AB})=\frac{1}{2}(10)=5\)$ (The line joining the mid-points of the two
sides of a triangle is parallel to the third side \& is half of it) Now, the area of triangle $\(\mathrm{ECF}=\frac{1}{2} \times\)$ Base $\(\times\)$ Height $\(=\frac{1}{2} \times \mathrm{EC} \times \mathrm{EF}=\frac{1}{2} \times 5 \times 5=12.5\)$
(As C is a mid - point of AC, EC must be half of AC)
Finally the area of the shaded portion $\(=\)$ area triangle $\(\mathrm{ABC}-\)$ area of triangle $\(\mathrm{ECF}=50-12.5=\)$ 37.5
Hence the answer is (B).

gmatclubot
Re: Each side of the square ABCD shown below is 10. What is the area of t [#permalink]
08 Mar 2025, 10:53
Moderators:



