GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If a circle with area 36 is inscribed in an equilateral triangle, wha
[#permalink]
29 Jun 2023, 01:14
29 Jun 2023, 01:14
Expert Reply
1
Bookmarks
00:00
Question Stats:
37% (02:21) correct
62% (01:18) wrong based on 8 sessions
Hide Show timer Statistics
If a circle with area \(36 \pi\) is inscribed in an equilateral triangle, what is the area of the triangle?
A. \(27 \sqrt{3}\)
B. \(54 \sqrt{3} \)
C. \(108 \sqrt{3}\)
D. \(144 \sqrt{3}\)
E. \(432 \sqrt{3} \)
Post A Detailed Correct Solution For The Above Questions And Get Kudos.
Question From Our Project: Free GRE Prep Club Tests in Exchange for 20 Kudos
\(\Longrightarrow\) GRE - Quant Daily Topic-wise Challenge
\(\Longrightarrow\) GRE GEOMETRY
A. \(27 \sqrt{3}\)
B. \(54 \sqrt{3} \)
C. \(108 \sqrt{3}\)
D. \(144 \sqrt{3}\)
E. \(432 \sqrt{3} \)
Post A Detailed Correct Solution For The Above Questions And Get Kudos.
Question From Our Project: Free GRE Prep Club Tests in Exchange for 20 Kudos
\(\Longrightarrow\) GRE - Quant Daily Topic-wise Challenge
\(\Longrightarrow\) GRE GEOMETRY
Re: If a circle with area 36 is inscribed in an equilateral triangle, wha
[#permalink]
16 Jul 2023, 10:12
16 Jul 2023, 10:12
Expert Reply
OE
Area of the circle = \(𝜋𝑟^2\) (r is the radius of the circle)
Given that area of circle = 36π
Hence, r = 6.
We know, when a circle is inscribed in an equilateral triangle, centroid of triangle is the
center of the circle, and centroid divided the median in the ratio 2:1.
i.e. AO: OD = 2:1
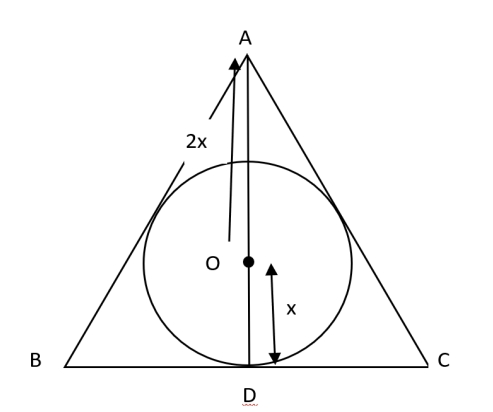
GRe triangle circle.jpg [ 29.57 KiB | Viewed 1295 times ]
Now, we know OD = 6, therefore AO = 12
Hence, median = height (of the equilateral triangle) = 6 + 12 = 18
Also, the height of an equilateral triangle \(= \dfrac{\sqrt{3}}{2} \times side=18\)
\(side = \dfrac{36}{\sqrt{3}}\)
Therefore, area of the triangle \(= \dfrac{3}{4} \times side^2= \dfrac{\sqrt{3}}{4} \times \dfrac{36}{\sqrt{3}} \times \dfrac{36}{\sqrt{3}}= 108 \sqrt{3}\)
C is the answer
Area of the circle = \(𝜋𝑟^2\) (r is the radius of the circle)
Given that area of circle = 36π
Hence, r = 6.
We know, when a circle is inscribed in an equilateral triangle, centroid of triangle is the
center of the circle, and centroid divided the median in the ratio 2:1.
i.e. AO: OD = 2:1
Attachment:
GRe triangle circle.jpg [ 29.57 KiB | Viewed 1295 times ]
Now, we know OD = 6, therefore AO = 12
Hence, median = height (of the equilateral triangle) = 6 + 12 = 18
Also, the height of an equilateral triangle \(= \dfrac{\sqrt{3}}{2} \times side=18\)
\(side = \dfrac{36}{\sqrt{3}}\)
Therefore, area of the triangle \(= \dfrac{3}{4} \times side^2= \dfrac{\sqrt{3}}{4} \times \dfrac{36}{\sqrt{3}} \times \dfrac{36}{\sqrt{3}}= 108 \sqrt{3}\)
C is the answer
gmatclubot
Re: If a circle with area 36 is inscribed in an equilateral triangle, wha [#permalink]
16 Jul 2023, 10:12
Moderators:
