GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
If ABC is a straight line as shown in the figure below, and the angles
[#permalink]
22 Sep 2021, 02:49
22 Sep 2021, 02:49
Expert Reply
00:00
Question Stats:
56% (01:24) correct
43% (01:09) wrong based on 16 sessions
Hide Show timer Statistics
If ABC is a straight line as shown in the figure below, and the angles x & y are integer multiples of 20, what is the value of x?
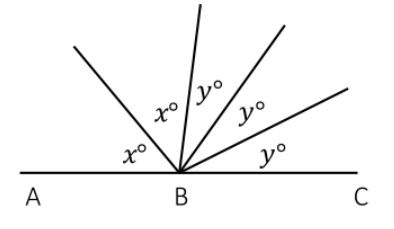
screenshot.124.jpg [ 17.37 KiB | Viewed 3046 times ]
A. 20
B. 40
C. 60
d. 80
E. 100
Source: manhattanreview
Attachment:
screenshot.124.jpg [ 17.37 KiB | Viewed 3046 times ]
A. 20
B. 40
C. 60
d. 80
E. 100
Source: manhattanreview
Retired Moderator
Joined: 19 Nov 2020
Posts: 326
Given Kudos: 64
GRE 1: Q160 V152
Re: If ABC is a straight line as shown in the figure below, and the angles
[#permalink]
22 Sep 2021, 08:05
22 Sep 2021, 08:05
1
\(2x+3y=180\)
factor of 20 should be distributed to LHS and RHS (left and right hand sides) of the above expression, rewritten as \(2x+2y=180-y\), \(x+y=90-y/2\). Notice that x and y are still divisible by 20, but 90 is not divisible by 20. For 90 to be divisible by 20, it must be reduced to either 80, 60, 40 or 20
Let's pick 80 as RHS value of \(x+y=90-y/2\), then \(90-y/2=80\) and y=20
When y=20 along with \(x+y=80\), x=60. Hence, x=60 and y=20
**
If we pick 60 as nextRHS value of \(x+y=90-y/2\), then \(90-y/2=60\) and y=60
When y=60 along with \(x+y=60\), x=0. Hence, x=0 and y=60 REJECT
**
Answer is C
Note: the additional solution between two up and down stars helps if the question is conversed into QC type.
factor of 20 should be distributed to LHS and RHS (left and right hand sides) of the above expression, rewritten as \(2x+2y=180-y\), \(x+y=90-y/2\). Notice that x and y are still divisible by 20, but 90 is not divisible by 20. For 90 to be divisible by 20, it must be reduced to either 80, 60, 40 or 20
Let's pick 80 as RHS value of \(x+y=90-y/2\), then \(90-y/2=80\) and y=20
When y=20 along with \(x+y=80\), x=60. Hence, x=60 and y=20
**
If we pick 60 as nextRHS value of \(x+y=90-y/2\), then \(90-y/2=60\) and y=60
When y=60 along with \(x+y=60\), x=0. Hence, x=0 and y=60 REJECT
**
Answer is C
Note: the additional solution between two up and down stars helps if the question is conversed into QC type.
Carcass wrote:
If ABC is a straight line as shown in the figure below, and the angles x & y are integer multiples of 20, what is the value of x?
A. 20
B. 40
C. 60
d. 80
E. 100
Source: manhattanreview
Attachment:
screenshot.124.jpg
A. 20
B. 40
C. 60
d. 80
E. 100
Source: manhattanreview
Re: If ABC is a straight line as shown in the figure below, and the angles
[#permalink]
22 Sep 2021, 12:43
22 Sep 2021, 12:43
any easy solution to above problem.
