
GRE Prep Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
GRE Quant - Absolute Values/Modulus Theory
[#permalink]
 07 Jun 2020, 08:11
07 Jun 2020, 08:11
3
Expert Reply
3
Bookmarks
Frequency of the concepts tested: Medium
Definition
The absolute value (or modulus) \(|x|\) of a real number x is x's numerical value without regard to its sign.
For example, \(|3| = 3\); \(|-12| = 12\); \(|-1.3|=1.3\)
Graph:
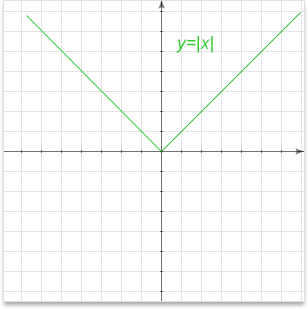
Important properties:
\(|x|\geq0\)
\(|0|=0\)
\(|-x|=|x|\)
\(|x|+|y|\geq|x+y|\)
\(|x|\geq0\)
How to approach equations with moduli
It's not easy to manipulate with moduli in equations. There are two basic approaches that will help you out. Both of them are based on two ways of representing modulus as an algebraic expression.
1) \(|x| = \sqrt{x^2}\). This approach might be helpful if an equation has × and /.
2) |x| equals x if x>=0 or -x if x<0. It looks a bit complicated but it's very powerful in dealing with moduli and the most popular approach too (see below).
3-steps approach:
General approach to solving equalities and inequalities with absolute value:
1. Open modulus and set conditions.
To solve/open a modulus, you need to consider 2 situations to find all roots:
For example, \(|x-1|=4\)
a) Positive: if \((x-1)\geq0\), we can rewrite the equation as: \(x-1=4\)
b) Negative: if \((x-1)<0\), we can rewrite the equation as: \(-(x-1)=4\)
We can also think about conditions like graphics. \(x=1\) is a key point in which the expression under modulus equals zero. All points right are the first condition \((x>1)\) and all points left are second condition \((x<1)\).
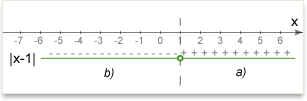
2. Solve new equations:
a) \(x-1=4\) --> x=5
b) \(-x+1=4\) --> x=-3
3. Check conditions for each solution:
a) \(x=5\) has to satisfy initial condition \(x-1>=0\). \(5-1=4>0\). It satisfies. Otherwise, we would have to reject x=5.
b) \(x=-3\) has to satisfy initial condition \(x-1<0\). \(-3-1=-4<0\). It satisfies. Otherwise, we would have to reject x=-3.
3-steps approach for complex problems
Let’s consider following examples,
Example #1
Q.: \(|x+3| - |4-x| = |8+x|\). How many solutions does the equation have?
Solution: There are 3 key points here: -8, -3, 4. So we have 4 conditions:
a) \(x < -8\). \(-(x+3) - (4-x) = -(8+x)\) --> \(x = -1\). We reject the solution because our condition is not satisfied (-1 is not less than -8)
b) \(-8 \leq x < -3\). \(-(x+3) - (4-x) = (8+x)\) --> \(x = -15\). We reject the solution because our condition is not satisfied (-15 is not within (-8,-3) interval.)
c) \(-3 \leq x < 4\). \((x+3) - (4-x) = (8+x)\) --> \(x = 9\). We reject the solution because our condition is not satisfied (9 is not within (-3,4) interval.)
d) \(x \geq 4\). \((x+3) + (4-x) = (8+x)\) --> \(x = -1\). We reject the solution because our condition is not satisfied (-1 is not more than 4)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
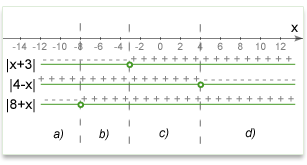
Answer: 0
Example #2
Q.: \(|x^2-4| = 1\). What is x?
Solution: There are 2 conditions:
a) \((x^2-4)\geq0\) --> \(x \leq -2\) or \(x\geq2\). \(x^2-4=1\) --> \(x^2 = 5\). x e {\(-\sqrt{5}\), \(\sqrt{5}\)} and both solutions satisfy the condition.
b) \((x^2-4)<0\) --> \(-2 < x < 2\). \(-(x^2-4) = 1\) --> \(x^2 = 3\). x e {\(-\sqrt{3}\), \(\sqrt{3}\)} and both solutions satisfy the condition.
(Optional) The following illustration may help you understand how to open modulus at different conditions.
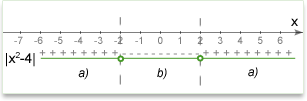
Answer: \(-\sqrt{5}\), \(-\sqrt{3}\), \(\sqrt{3}\), \(\sqrt{5}\)
Tip & Tricks
The 3-steps method works in almost all cases. At the same time, often there are shortcuts and tricks that allow you to solve absolute value problems in 10-20 sec.
I. Thinking of inequality with modulus as a segment at the number line.
For example,
Problem: 1<x<9. What inequality represents this condition?

A. |x|<3
B. |x+5|<4
C. |x-1|<9
D. |-5+x|<4
E. |3+x|<5
Solution: 10sec. Traditional 3-steps method is too time-consume technique. First of all we find length (9-1)=8 and center (1+8/2=5) of the segment represented by 1<x<9. Now, let’s look at our options. Only B and D has 8/2=4 on the right side and D had left site 0 at x=5. Therefore, answer is D.
II. Converting inequalities with modulus into a range expression.
In many cases, especially in DS problems, it helps avoid silly mistakes.
For example,
|x|<5 is equal to x e (-5,5).
|x+3|>3 is equal to x e (-inf,-6)&(0,+inf)
III. Thinking about absolute values as the distance between points at the number line.
For example,
Problem: A<X<Y<B. Is |A-X| <|X-B|?
1) |Y-A|<|B-Y|
Solution:
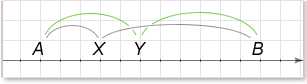
We can think of absolute values here as the distance between points. Statement 1 means than the distance between Y and A is less than that between Y and B. Because X is between A and Y, |X-A| < |Y-A| and at the same time the distance between X and B will be larger than that between Y and B (|B-Y|<|B-X|). Therefore, statement 1 is sufficient.
Pitfalls
The most typical pitfall is ignoring the third step in opening modulus - always check whether your solution satisfies conditions.
The absolute value (or modulus) \(|x|\) of a real number x is x's numerical value without regard to its sign.
For example, \(|3| = 3\); \(|-12| = 12\); \(|-1.3|=1.3\)
Graph:
Important properties:
\(|x|\geq0\)
\(|0|=0\)
\(|-x|=|x|\)
\(|x|+|y|\geq|x+y|\)
\(|x|\geq0\)
How to approach equations with moduli
It's not easy to manipulate with moduli in equations. There are two basic approaches that will help you out. Both of them are based on two ways of representing modulus as an algebraic expression.
1) \(|x| = \sqrt{x^2}\). This approach might be helpful if an equation has × and /.
2) |x| equals x if x>=0 or -x if x<0. It looks a bit complicated but it's very powerful in dealing with moduli and the most popular approach too (see below).
3-steps approach:
General approach to solving equalities and inequalities with absolute value:
1. Open modulus and set conditions.
To solve/open a modulus, you need to consider 2 situations to find all roots:
- Positive (or rather non-negative)
- Negative
For example, \(|x-1|=4\)
a) Positive: if \((x-1)\geq0\), we can rewrite the equation as: \(x-1=4\)
b) Negative: if \((x-1)<0\), we can rewrite the equation as: \(-(x-1)=4\)
We can also think about conditions like graphics. \(x=1\) is a key point in which the expression under modulus equals zero. All points right are the first condition \((x>1)\) and all points left are second condition \((x<1)\).
2. Solve new equations:
a) \(x-1=4\) --> x=5
b) \(-x+1=4\) --> x=-3
3. Check conditions for each solution:
a) \(x=5\) has to satisfy initial condition \(x-1>=0\). \(5-1=4>0\). It satisfies. Otherwise, we would have to reject x=5.
b) \(x=-3\) has to satisfy initial condition \(x-1<0\). \(-3-1=-4<0\). It satisfies. Otherwise, we would have to reject x=-3.
3-steps approach for complex problems
Let’s consider following examples,
Example #1
Q.: \(|x+3| - |4-x| = |8+x|\). How many solutions does the equation have?
Solution: There are 3 key points here: -8, -3, 4. So we have 4 conditions:
a) \(x < -8\). \(-(x+3) - (4-x) = -(8+x)\) --> \(x = -1\). We reject the solution because our condition is not satisfied (-1 is not less than -8)
b) \(-8 \leq x < -3\). \(-(x+3) - (4-x) = (8+x)\) --> \(x = -15\). We reject the solution because our condition is not satisfied (-15 is not within (-8,-3) interval.)
c) \(-3 \leq x < 4\). \((x+3) - (4-x) = (8+x)\) --> \(x = 9\). We reject the solution because our condition is not satisfied (9 is not within (-3,4) interval.)
d) \(x \geq 4\). \((x+3) + (4-x) = (8+x)\) --> \(x = -1\). We reject the solution because our condition is not satisfied (-1 is not more than 4)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
Answer: 0
Example #2
Q.: \(|x^2-4| = 1\). What is x?
Solution: There are 2 conditions:
a) \((x^2-4)\geq0\) --> \(x \leq -2\) or \(x\geq2\). \(x^2-4=1\) --> \(x^2 = 5\). x e {\(-\sqrt{5}\), \(\sqrt{5}\)} and both solutions satisfy the condition.
b) \((x^2-4)<0\) --> \(-2 < x < 2\). \(-(x^2-4) = 1\) --> \(x^2 = 3\). x e {\(-\sqrt{3}\), \(\sqrt{3}\)} and both solutions satisfy the condition.
(Optional) The following illustration may help you understand how to open modulus at different conditions.
Answer: \(-\sqrt{5}\), \(-\sqrt{3}\), \(\sqrt{3}\), \(\sqrt{5}\)
Tip & Tricks
The 3-steps method works in almost all cases. At the same time, often there are shortcuts and tricks that allow you to solve absolute value problems in 10-20 sec.
I. Thinking of inequality with modulus as a segment at the number line.
For example,
Problem: 1<x<9. What inequality represents this condition?
A. |x|<3
B. |x+5|<4
C. |x-1|<9
D. |-5+x|<4
E. |3+x|<5
Solution: 10sec. Traditional 3-steps method is too time-consume technique. First of all we find length (9-1)=8 and center (1+8/2=5) of the segment represented by 1<x<9. Now, let’s look at our options. Only B and D has 8/2=4 on the right side and D had left site 0 at x=5. Therefore, answer is D.
II. Converting inequalities with modulus into a range expression.
In many cases, especially in DS problems, it helps avoid silly mistakes.
For example,
|x|<5 is equal to x e (-5,5).
|x+3|>3 is equal to x e (-inf,-6)&(0,+inf)
III. Thinking about absolute values as the distance between points at the number line.
For example,
Problem: A<X<Y<B. Is |A-X| <|X-B|?
1) |Y-A|<|B-Y|
Solution:
We can think of absolute values here as the distance between points. Statement 1 means than the distance between Y and A is less than that between Y and B. Because X is between A and Y, |X-A| < |Y-A| and at the same time the distance between X and B will be larger than that between Y and B (|B-Y|<|B-X|). Therefore, statement 1 is sufficient.
Pitfalls
The most typical pitfall is ignoring the third step in opening modulus - always check whether your solution satisfies conditions.
The absolute value of a number is the value of a number without regard to its sign.
For example, \(|3| = 3\); \(|-12| = 12\); \(|-1.3|=1.3\)...
Another way to understand absolute value is as the distance from zero. For example, \(|x|\) is the distance between x and 0 on a number line.
From that comes the most important property of an absolute value: since the distance cannot be negative, an absolute value expression is ALWAYS more than or equal to zero.
GRAPH OF y=|x|
As you can see for any value of x, the value of y, which is |x|, is ALWAYS more than or equal to zero.
IMPORTANT PROPERTY
When \(x\leq{0}\), then \(|x|=-x\), or more generally when \(some \ expression\leq{0}\) then \(|some \ expression|={-(some \ expression)}\). For example: \(|-5|=5=-(-5)\). Notice that in the negative scenario, we don't simply remove the absolute value bars. We remove the absolute value bars and negate the entire expression contained within, thus making it positive again;
When \(x\geq{0}\), then \(|x|=x\), or more generally when \(some \ expression\geq{0}\) then \(|some \ expression|={some \ expression}\). For example: \(|5|=5\).
OTHER IMPORTANT PROPERTIES
1. \(|x|\geq0\)
2. \(\sqrt{x^2}=|x|\)
3. \(|0|=0\)
4. \(|-x|=|x|\)
5. \(|x-y|=|y-x|\). |x - y| represents the distance between x and y, so naturally it equals to |y - x|, which is the distance between y and x.
6. \(|x|+|y|\geq|x+y|\). Note that "=" sign holds for \(xy\geq{0}\) (or simply when \(x\) and \(y\) have the same sign). So, the strict inequality (>) holds when \(xy<0\);
7. \(|x|-|y|\leq{|x-y|}\). Note that "=" sign holds for \(xy>{0}\) (so when \(x\) and \(y\) have the same sign) and \(|x|\geq{|y|}\) (simultaneously).
Re: GRE Quant - Absolute Values/Modulus Theory
[#permalink]
 07 Jun 2020, 08:16
07 Jun 2020, 08:16
1
Expert Reply
1
Bookmarks
| FROM Veritas Prep Blog: Properties of Absolute Values |
 We have talked about quite a few concepts involving absolute value of x in our previous posts. But some absolute value questions involve two variables. Then do we need to consider the positive and negative values of both x and y? Certainly! But there are some properties of absolute value that could come in handy in such questions. Let’s take a look at them: (I) For all real x and y, |x + y| <= |x| + |y| (II) For all real x and y, |x – y| >= |x| – |y| We don’t need to learn them of course and there is no need to look at how to prove them either. All we need to do is understand them – why do they hold, when is the equality sign applicable and when can they be useful. Let’s look at both the properties one by one. (I) For all real x and y, |x + y| <= |x| + |y| The result of both the left hand side and the right hand side will be positive or zero. On the right hand side, the absolute values of x and y will always get added irrespective of the signs of x and y. On the left hand side, the absolute values of x and y might get added or subtracted depending on whether they have the same sign or different signs. Hence the result of the left hand side might be smaller than or equal to that of the right hand side. For which values of x and y will the equality hold and for which values will the inequality hold? Let’s think logically about it. The absolute values of x and y get added on the right hand side. We want the absolute values of x and y to get added on the left hand side too for the equality to hold. This will happen when x and y have the same sign. So the equality should hold when they have the same signs. For example, x = 4, y = 8: |4 + 8| = |4| + |8| = 12 OR x = -3, y = -4: |-3 -4| = |-3| + |-4| = 7 Also, when at least one of x and y is 0, the equality will hold. For example, x = 0, y = 8: |0 + 8| = |0| + |8| = 8 OR x = -3, y = 0: |-3 + 0| = |-3| + |0| = 3 What happens when x and y have opposite signs? On the left hand side, the absolute values of x and y get subtracted hence the left hand side will be smaller than the right hand side (where they still get added). That is when the inequality holds i.e. |x + y| < |x| + |y| For example, x = -4, y = 8: |-4 + 8| < |-4| + |8| 4 < 12 OR x = 3, y = -4: |3 -4| < |3| + |-4| 1 < 7 Let’s look at our second property now: (II) For all real x and y, |x – y| >= |x| – |y| Thinking on similar lines as above, we see that the right hand side of the inequality will always lead to subtraction of the absolute values of x and y whereas the left hand side could lead to addition or subtraction depending on the signs of x and y. The left hand side will always be positive whereas the right hand side could be negative too. So in any case, the left hand side will be either greater than or equal to the right hand side. When will the equality hold? When x and y have the same sign and x has greater (or equal) absolute value than y, both sides will yield a positive result which will be the difference between their absolute values For example, x = 9, y = 2; |9 – 2| = |9| – |2| = 7 OR x = -7, y = -3 |-7 – (-3)| = |-7| – |-3| = 4 Also when y is 0, the equality will hold. For example, x = 8, y = 0: |8 – 0| = |8| – |0| = 8 OR x = -3, y = 0: |-3 – 0| = |-3| – |0| = 3 What happens when x and y have the same sign but absolute value of y is greater than that of x? It is easy to see that in that case both sides have the same absolute value but the right hand side becomes negative. For example, x = -4, y = -9 |x – y| = |-4 – (-9)| = 5 |x| – |y| = |-4| – |-9| = -5 So even though the absolute values will be the same since we will get the difference of the absolute values of x and y on both sides, the right hand side will be negative. If we were to take further absolute value of the right hand side, the two will become equal i.e. the right hand side will become |(|x| – |y|)| = |-5| = 5 in our example above. In that case, the equality will hold again. Similarly, what happens when only x = 0? The right hand side becomes negative again so taking further absolute value will make both sides equal. For example, x = 0, y = -5 |x – y| = |0 – (-5)| = 5 |x| – |y| = |0| – |5| = -5 Taking further absolute value, |(|x| – |y|)| = |-5| = 5 So when we take further absolute value of the right hand side, this property becomes similar to property 1 above: |x – y| = |(|x| – |y|)| when x and y have the same sign or at least one of x and y is 0. Now let’s look at the inequality part of property 2. Whenever x and y have opposite signs, |x – y| > |x| – |y| On the left hand side, the absolute values will get added while on the right hand side, the absolute values will get subtracted. So the absolute value of the left hand side will always be greater than the absolute value of the right hand side. The left hand side will always be positive while the right hand side could be negative too. Hence even if we take the further absolute value of the right hand side, the inequality will hold: |x – y| > |(|x| – |y|)| when x and y have opposite signs For example, x = -4, y = 8: |-4 – 8| > |-4| – |8| 12 > -4 Taking further absolute value of the right hand side, we get |(|x| – |y|)| = |-4| = 4 Still, 12 > 4 i.e. |x – y| > |(|x| – |y|)| OR x = 3, y = -4: |3 –(-4)| > |3| – |-4| 7 > -1 Taking further absolute value of the right hand side, we get |(|x| – |y|)| = |-1| = 1 Still, 7 > 1 i.e. |x – y| > |(|x| – |y|)| Note that the inequality of the original property 2 also holds when x and y have the same sign but absolute value of y is greater than the absolute value of x since the right hand side becomes negative. It also holds when x is 0 but y is not. To sum it all neatly, (I) For all real x and y, |x + y| <= |x| + |y| |x + y| = |x| + |y| when (1) x and y have the same sign (2) at least one of x and y is 0. |x + y| < |x| + |y| when (1) x and y have opposite signs (II) For all real x and y, |x – y| >= |x| – |y| |x – y| = |x| – |y|when (1) x and y have the same sign and x has greater (or equal) absolute value than y (2) y is 0 |x – y| > |x| – |y| in all other cases (III) For all real x and y, |x – y| >= |(|x| – |y|)| |x – y| = |(|x| – |y|)| when (1) x and y have the same sign (2) at least one of x and y is 0. |x – y| > |(|x| – |y|)| when (1) x and y have opposite signs Note that property (III) matches property (I). There is another property we would like to discuss but let’s take it up next week along with some GMAT questions where we put these properties to use. Karishma, a Computer Engineer with a keen interest in alternative Mathematical approaches, has mentored students in the continents of Asia, Europe and North America. She teaches the GMAT for Veritas Prep and regularly participates in content development projects such as this blog! |
ForumBlogs - GMAT Club’s latest feature blends timely Blog entries with forum discussions. Now GMAT Club Forums incorporate all relevant information from Student, Admissions blogs, Twitter, and other sources in one place. You no longer have to check and follow dozens of blogs, just subscribe to the relevant topics and forums on GMAT club or follow the posters and you will get email notifications when something new is posted. Add your blog to the list! and be featured to over 300,000 unique monthly visitors
Re: GRE Quant - Absolute Values/Modulus Theory
[#permalink]
 07 Jun 2020, 08:18
07 Jun 2020, 08:18
Expert Reply
1
Bookmarks
| FROM Veritas Prep Blog: Properties of Absolute Values II |
 We pick up this post from where we left the post of last week in which we looked at a few properties of absolute values in two variables. There is one more property that we would like to talk about today. Thereafter, we will look at a question based on some of these properties. (III) |x – y| = 0 implies x = y x and y could be positive/negative integer/fraction; if the absolute value of their difference is 0, it means x = y. They cannot have opposite signs while having the same absolute value. They must be equal. This also means that if and only if x = y, the absolute value of their difference will be 0. Mind you, this is different from ‘difference of their absolute values’ |x| – |y| = 0 implies that the absolute value of x is equal to the absolute value of y. So x and y could be equal or they could have opposite signs while having the same absolute value. Let’s now take up the question we were talking about. Question: Is |x + y| < |x| + |y|? Statement 1: | x | ≠ | y | Statement 2: | x – y | > | x + y | Solution: One of the properties we discussed last week was “For all real x and y, |x + y| <= |x| + |y| |x + y| = |x| + |y| when (1) x and y have the same sign (2) at least one of x and y is 0. |x + y| < |x| + |y| when (1) x and y have opposite signs” We discussed in detail the reason absolute values behave this way. So our question “Is |x + y| < |x| + |y|?” now becomes: Question: Do x and y have opposite signs? We do not care which one is greater – the one with the positive sign or the one with the negative sign. All we want to know is whether they have opposite signs (opposite sign also implies that neither one of x and y can be 0)? If we can answer this question definitively with a ‘Yes’ or a ‘No’, the statement will be sufficient to answer the question. Let’s go on to the statements now. Statement 1: | x | ≠ | y | This statement tells us that absolute value of x is not equal to absolute value of y. It doesn’t tell us anything about the signs of x and y and whether they are same or opposite. So this statement alone is not sufficient. Statement 2:| x – y | > | x + y | Let’s think along the same lines as last week – when will | x – y | be greater than | x + y |? When will the absolute value of subtraction of two numbers be greater than the absolute value of their addition? This will happen only when x and y have opposite signs. In that case, while subtracting, we would actually be adding the absolute values of the two and while adding, we would actually be subtracting the absolute values of the two. That is when the absolute value of the subtraction will be more than the absolute value of the addition. For Example: x = 3, y = -2 | x – y | = |3 – (-2)| = 5 | x + y | = |3 – 2| = 1 or x = -3, y = 2 | x – y | = |-3 – 2| = 5 | x + y | = |-3 + 2| = 1 If instead, x and y have the same sign, | x + y | will be greater than| x – y |. If at least one of x and y is 0, | x + y | will be equal to| x – y |. Since this statement tells us that | x – y | > | x + y |, it implies that x and y have opposite signs. So this statement alone is sufficient to answer the question with a ‘Yes’. Answer (B) Takeaway from this question: If x and y have the same signs, | x + y | >| x – y |. If x and y have opposite signs, | x + y | <| x – y |. If at least one of x and y is 0, | x + y | =| x – y |. You don’t need to ‘learn this up’. Understand the logic here. You can easily recreate it in the exam if need be. Karishma, a Computer Engineer with a keen interest in alternative Mathematical approaches, has mentored students in the continents of Asia, Europe and North America. She teaches the GMAT for Veritas Prep and regularly participates in content development projects such as this blog! |
ForumBlogs - GMAT Club’s latest feature blends timely Blog entries with forum discussions. Now GMAT Club Forums incorporate all relevant information from Student, Admissions blogs, Twitter, and other sources in one place. You no longer have to check and follow dozens of blogs, just subscribe to the relevant topics and forums on GMAT club or follow the posters and you will get email notifications when something new is posted. Add your blog to the list! and be featured to over 300,000 unique monthly visitors











